A sense of proportion

Two variables are said to be in proportion if the change in one can be predicted from a change in the other. There are two distinct types of proportional relationship relevant to secondary school chemists: direct and inverse proportion. Direct proportion is conceptually easier – for example, if we double the volume of a solid, we also double its mass.

This idea can, of course, be translated into mathematical notation. Suppose that when the variable x is 1, a corresponding variable y has the value 3; and when x is doubled so that its value is 2, y also doubles so its value is 6. We might then speculate that when x is 3, y would have the value 9. This would indeed be the case if x is directly proportional to y.

The ratio of y to x is therefore constant:

and this constant ratio is known as the 'constant of proportionality'. Indeed, the test of whether two variables are in direct proportion is whether they have a constant ratio. In other words, if we divide the value of one variable by another, do we obtain the same value each time? If the answer is yes the variables vary in direct proportion to one another, which we can write as

y∝ x

If we denote this constant of proportionality by k, we have

Multiplying both sides by x then gives

y = kx

This can be compared with the general equation of a straight line

y = mx + c

with gradient m = k and intercept c = 0. Therefore, if two quantities are in direct proportion, a graph of one against the other will be a straight line passing through the origin (fig1).

Direct proportion in chemistry

An interesting example of this is the Beer-Lambert law, which allows us to calculate the extent to which light is absorbed when it passes through a solution. This absorbance, A, is given by the equation

A =εcl

Note that we are now using c to represent concentration of the solution, and l represents the path length, which is the distance the light travels through the solution. The other term in the equation, ε, is the molar absorption coefficient and is a constant. For a given spectrometer, measuring different solutions of the same substance, the path length and molar absorption coefficients will both be constant, so multiplying them together also gives a constant εl. Dividing both sides of the equation by c gives

and since this ratio is a constant, A is directly proportional to c.

For example: the absorbance of a 0.01 mol dm^-3 solution of bromine in tetrachloromethane is 0.55.¹ The absorbance of a 0.02 mol dm^–3 solution is therefore 1.1; if we double the concentration, the absorbance doubles, owing to the directly proportional relationship between the two variables.

Inverse proportion

If two variables are in inverse proportion, when we double one the other is halved. If x = 4 when y = 12, and doubling x to 8 results in y being halved to 6, we might expect that x is inversely proportional to y. If this was the case, then doubling x again to 16 should result in y being halved again to 3. In this case the product of the two variables remains constant

xy = 4 x 12 = 8 x 6 = 16 x 3 = 48

and we can write

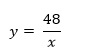
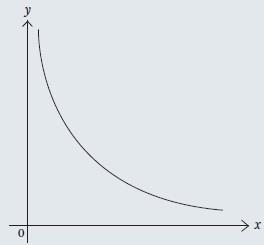
The graphical representation of two inversely proportional variables is less useful than for direct proportionalilty, resulting in a curve (Fig2).

Inverse proportion in chemistry

This idea is of fundamental importance in the laboratory when we dilute concentrated solutions. The concentration, c, of a solution is given by

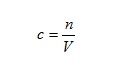
where n is the amount of solute and V the volume of solution. If we multiply both sides of this equation by V we have

n = cV

Consider for a moment the process of diluting a solution. We begin with a certain volume of solution, and then add more solvent. Thus the amount of substance, n, will remain constant while the volume, V, and concentration, c, change in inverse proportion to each other.

If we start with volume V₁ at concentration c₁, and dilute to volume V₂ at concentration c_2, the value of n remains constant, so we have

c₁V₁ = c₂V₂

If we divide both sides of this equation by V_2, we have

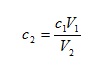
so we can calculate the concentration of any diluted solution given the starting concentration and an initial and final volume. On the other hand, if we divide both sides by c_2, we have

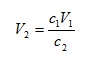
so we can determine the final volume required to give a solution of specified concentration c₂.

Suppose 6.7 cm³ of sulfuric acid² of initial concentration 0.15 mol dm^-3 was diluted to 16.5 cm³. We have

V₁ = 6.7 cm³

V₂ = 16.5 cm³

c₁ = 0.15 mol dm^-3

We can therefore calculate the final concentration from

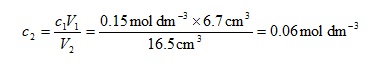
There are two things to note here. First, the units of V₁ and V₂ cancel, leaving us with c₁ and c₂ having the same units. Second, we would expect the concentration of the diluted solution to be less than the initial one, which is the case. It is possible to become sufficiently proficient at these calculations that they can be performed by intuition rather than by using the formal derived equation.

Suppose that we wish to obtain a 0.2 mol dm^-3 solution of ammonia,² starting with 500 cm³ of a 0.5 mol dm^-3 solution. We can calculate the final volume required from

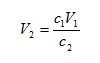
with

c₁ = 0.5 mol dm^-3

c₂ = 0.2 mol dm^-3

V₁ = 500 cm³

so that

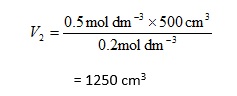
This time, of course, we expect to obtain a larger volume of diluted solution. It is important to remember that this is the final volume of solution, so the amount of water that needs to be added is obtained by subtracting the initial volume of solution from the final total

1250 cm³– 500 cm³ = 750 cm³

Linda Fisher of Florida State University, US, has investigated the strategies used by secondary mathematics teachers to solve proportion problems,³ and found that most tend to use an algebraic approach (as outlined here) rather than less formal methods. Susan Lamon notes that the term 'proportional reasoning' is ill defined,⁴ and that its mastery remains as an ill-defined by-product of teaching fractions. She also states that while it requires an understanding of relatively elementary mathematical ideas, it provides the foundation for an understanding of much more complex topics. Jane-Jane Lo, Jinfa Cai and Tad Watanabe have provided an interesting comparison of how the topic is treated by textbooks from three Asian regions and the United States.⁵ The textbooks differ in their definition of the term ratio, the way equal ratios are introduced and the type of application problems included.

Paul Yates is strategic academic development adviser at the University of Chester, UK