Reflecting on symmetry

The concept of symmetry is introduced in GCSE mathematics, but provides an incredibly powerful tool for understanding molecular behaviour in topics such as spectroscopy and quantum mechanics. The way that simple symmetry elements apply to molecular structures can be introduced by working in two dimensions and considering planar molecules.

Teaching aids

Extending these principles to three dimensions is much easier using molecular models, and hand-held models probably have an advantage over computer generated ones.¹ Recent advances in 3D printing provide interesting opportunities in this area.²

However, more homemade teaching aids can be just as effective, for example: a collection of objects showing different symmetry; a magnet-backed mirror and a set of modified molecular models; and a frame to demonstrate different symmetry axes.³

Xenia Xistouri and Demetra Pitta-Pantazi from the University of Cyprus have suggested students’ mathematical performance in reflective symmetry tasks can be predicted by their general mathematical achievement, perspective taking abilities and spatial rotation abilities, in descending order of importance.⁴ Ji-Won Son from the State University of New York in Buffalo, US, has also suggested that there is confusion between reflection and rotation among both students and pre-service teachers.⁵

We saw in a previous article⁶ that the position of any point (and consequently any atom) can be defined in terms of its x and y coordinates, denoted as (x,y). If we can understand the behaviour of individual points when symmetry operations are applied, and identify appropriate symmetry elements (mirror planes, rotational axes and inversion centres), then we will be able to combine several points and study molecules.

Note that where the absolute value of a number is referred to, this is simply its magnitude without taking account of whether it is positive or negative. Thus, the absolute value of both 2 and –2 is 2.

Reflection symmetry

Consider the behaviour of a point (1,2).

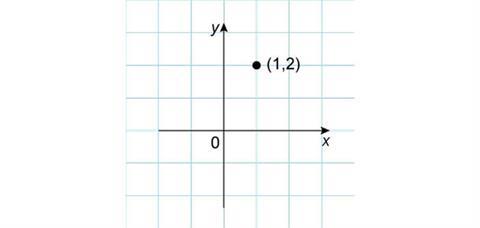
First, observe what happens when this point is reflected in the x-axis. The x-coordinate remains the same, while the y-coordinate changes from positive to negative with the same absolute value. The new coordinates of the point are then (1,–2).

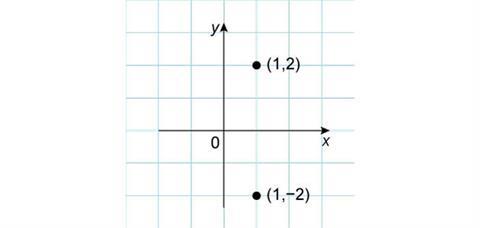
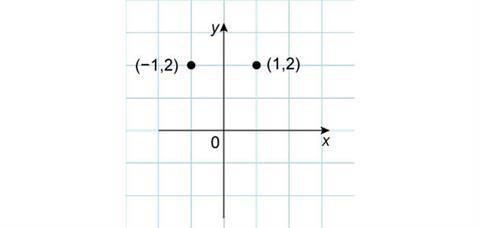
Similar arguments apply if the original point is reflected in the y-axis. This time the y-coordinate stays the same, while the x-coordinate becomes negative and the new coordinates are (–1,2).

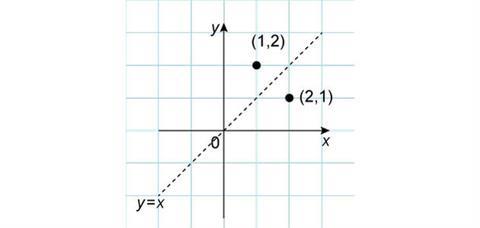
A final reflection that is also useful to consider is in the line y = x. It is probably easiest to consider this by drawing appropriate lines on graph paper, which will show that the new x-coordinate takes the value of the original y-coordinate and vice versa. This gives new coordinates of (2,1).

Reflection symmetry elements (usually described as planes in 3D) are denoted by the Greek letter s (sigma). This is often accompanied by a subscript to specify more precisely, for example s_v and s_h denote vertical and horizontal mirror planes.

Rotation symmetry

To consider rotational symmetry of our point, it is probably easiest to consider it moving in a circle centred on the origin. If we rotate it by 180°, we reach the point (–1,–2). Here, both the original coordinates have become negative.

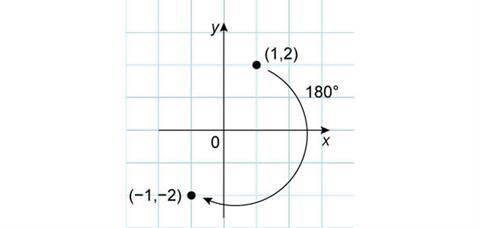
If the rotation was only 90° then the new point is (2,–1). The coordinate transformation is less obvious, but the absolute values of the x and y-coordinates have been exchanged and the new y-coordinate switches sign.

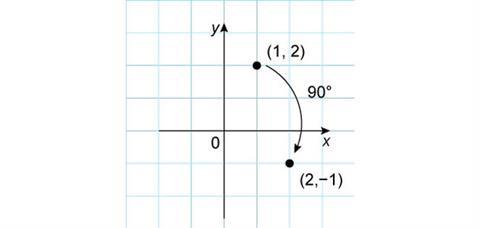
We could clearly rotate a point through any angle, but the transformation of the coordinates will be harder to describe.

We could clearly rotate a point through any angle, but the transformation of the coordinates will be harder to describe.

Inversion about the origin

The inversion operation simply reverses the sign on all the coordinates. This means that our original point moves from (1,2) to (–1,–2). In this case this is the same as a 180° rotation, but generally these two operations may give different results. The inversion symmetry element is denoted by the symbol i.

Molecular symmetry

Determining the symmetry elements present in a molecule involves considering which rotations, reflections and inversions will leave the shape of the molecule unchanged; even though individual atoms will have moved, the final result must be indistinguishable from the starting structure. The planar molecule ethene provides a simple example to demonstrate the effects of the symmetry elements described above. We can define the x-axis to run through the carbon-carbon double bond while the y-axis bisects this bond at right angles. The atoms have been given different labels to allow us to follow their transformations.

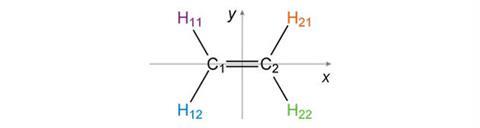
If we reflect the atoms in the x-axis we see that atoms C1 and C2 do not move position. H11 and H12 exchange, as do H21 and H22. The final result is indistinguishable from the starting structure, confirming that the x-axis (or more correctly the xz-plane perpendicular to the paper) is a vertical mirror plane, denoted sv.

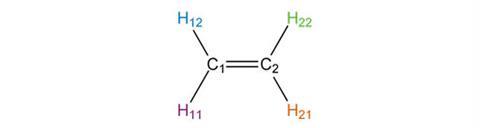
If we reflect in the y-axis, C1 and C2 are exchanged, as are the pairs H11 and H21, and H12 and H22. The result is also indistinguishable from our starting structure, so the y-axis (or yz-plane) is also a sv mirror plane.

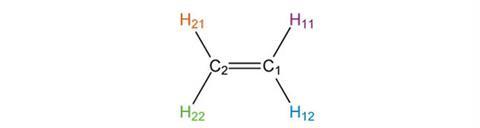
Because ethene is planar, it has a third plane of symmetry: the plane of the paper. Reflecting in this plane does not move any of the atoms in this case. This horizontal plane of symmetry is denoted sh.

Rotating ethene

Imagine a rotation axis that runs perpendicular to the page through the centre of the carbon–carbon double bond. Rotating the molecule by 90° leaves the carbon-carbon double bond oriented top-to-bottom on the page, where previously it was oriented left-to-right. This is different to the starting structure, so this operation does not represent a valid symmetry element for ethene.

However, rotating through 180° gives a structure that is indistinguishable from the starting position, in which C1 and C2, H11 and H22, and H12 and H21 have exchanged positions. We say that ethene possesses a C2 symmetry axis, the subscript 2 denoting that 2 rotations are required to restore all the atoms to their starting positions. Higher order rotational axes follow the same pattern, for example the trigonal planar molecule BF3 has a C3 rotation axis.

The effect of the C₂ operation gives the same structure as reflection in the y-axis. It is frequently the case that applying different symmetry elements results in the same arrangement of atoms.

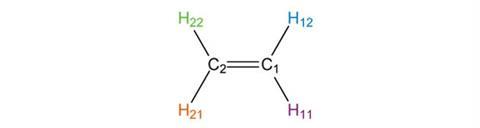
Ethene possesses two other C2 symmetry axes, along the x and y axes that we have defined. The first of these consequently runs along the C=C double bond.

Ethene inversion

Finally we can consider the inversion operation. While this involves changing the sign of each coordinate, we can think of the operation as moving each atom an equal distance the other side of the origin in a straight line. This is shown by the dotted lines linking H₁₁ and H₂₂, and H₁₂ and H₂₁. The final result is that these atoms exchange positions, as do C₁ and C₂. This structure is indistinguishable from the original position, confirming that the inversion element, or centre of symmetry, is also present.

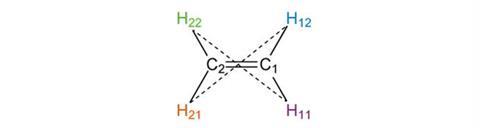
All molecules also contain the identity symmetry element, denoted E. This actually means ‘do nothing’, but must be included in any complete list of symmetry elements present.

The branch of mathematics concerned with symmetry elements and the way in which they combine is known as group theory.⁷ Together, the symmetry elements define a molecule’s point group, which can be used to predict whether spectroscopic transitions are allowed, mechanisms of organic reactions and solid state structures. The point group of ethene is D_2h, which it shares with other molecules such as transplatin, trans-[PtCl₂(NH₃)₂]. Grouping molecules according to point group helps to explain similarities in behaviour between apparently very different molecules.

Paul Yates is the director of learning and teaching at the University of Chester, UK