Trigonometry in chemistry

Given that chemistry takes place in three dimensions, it is of no surprise that trigonometry plays an important role in a mathematical description of the subject. Indeed, what may be most surprising is that only a very limited range of trigonometric skills is required by most chemists.

Measurement of angle

We normally measure angles in degrees, and this is the accepted convention when dealing with three dimensions in chemistry. However, there are other situations when a different angle unit is more convenient. This is the radian, which is related to the degree by the simple relationship

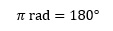
where π is the familiar constant which for most purposes can be taken as having the value of 3.142 or 22/7. 

The use of degrees and radians in trigonometry is not without its problems,¹ but for most purposes these can be ignored and the definition above is satisfactory. It leads immediately to further relationships such as:

A moment's thought will show that angles measured in radians have much lower values than those measured in degrees. This can be disorienting when met for the first time. The most important thing for students to remember is that electronic calculators can be set to operate in radian (RAD) or degree (DEG) mode, and that it is important to know how to switch from one to another and which mode is currently set.

The sine function

Most applications involving trigonometry in chemistry require use of the sine function. This is defined for an angle  in terms of the right angled triangle by the equation

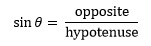
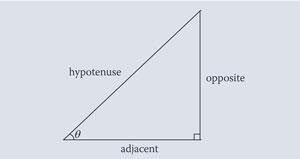
although other ways of introducing the function have been described.²

The graph of the sine function is shown below for angles from 0 to 360°. The function does in fact repeat itself every 360° or 2π rad and is defined for any angle, positive or negative and is therefore said to be periodic. It is also worth noting that it has an amplitude of 1, ie it ranges from -1 to 1. 

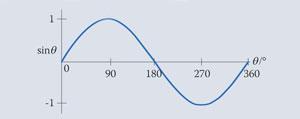
The function 2 sin θ has twice the amplitude of the original function, ie it is stretched in the vertical function so that it ranges from -2 to 2. 

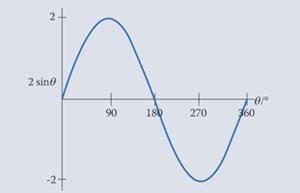
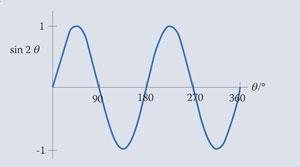
On the other hand, sin 2 θ has half the period, ie is compressed to half the width. 

Bragg's law

This is one of the most frequently met relationships in chemistry that involves a trigonometric function. It describes the way in which x-rays of wavelength λ are diffracted from the surface of a crystal in which the lattice planes are separated by a distance d. It is found that in this case the reflected x-ray beam appears at only certain angles θ; the first of these is described as the first order reflection with n = 1, the next as second order with n = 2, and so on. The equation which governs this behaviour is:

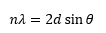
and the behaviour of the x-rays is usually represented by the following diagram:

Example

In a lithium fluoride crystal a set of lattice planes are separated by a distance of 201 pm.³ The first reflected beam (n  = 1) appears at an angle of 34.68°. We can calculate the wavelength λ of the x-rays by rearranging the previous equation to give: 

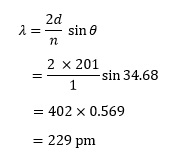
Notice that when we take the sine of an angle the result has no units. As n  also has no units, it is usual to give λ the same units as those quoted for d . 

It is also possible to use the Bragg equation to determine the angle θ at which x-rays are diffracted, but in order to do this we need to learn an additional technique. Consider the example of sodium chloride in which d  = 2.82 x 10^-10 m.⁴ If λ = 7.071 x 10^-11 m, the Bragg equation gives us

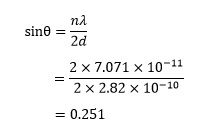
for second order reflections with n  = 2. As we would expect, the value of sin q  is less than 1, but we now need to convert it to the actual angle, θ. To do this, we need to invoke the use of an inverse function. Every function has its inverse, which essentially undoes the effect of the original function. 

In this case the relevant inverse function is known, not surprisingly, as the inverse sine function. The nomenclature for this is potentially problematic; the inverse of sin q is often written as sin^-1θ, but has nothing to do with the reciprocal. This is how such inverse functions are usually represented on electronic calculators. An alternative notation for the inverse of sin θ is arcsin θ. 

Applying this to the current example allows us to rewrite the expression:

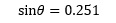
as:

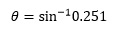
Use of the calculator then gives us:

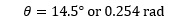
depending on the mode being used as explained earlier. 

Spectroscopy - an application

It is probably more surprising that the sine function plays a role in one of the ways of predicting spectroscopic data for hexatriene. This is actually due to the periodic nature of the sine function, which means that it can be used in one of the simplest quantum mechanical treatments of molecules. 

We need to assume that the electrons in hexatriene are constrained to move in a one dimensional box of length 7.3 x 10^-10 m.⁵ The theory can be developed to predict that the six delocalised electrons can only occupy a number of discrete energy levels; the behaviour of the electron in each is described by an equation of the form

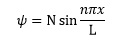
Where N is a constant, L = 7.3 x 10^-10 m, n  can take integer values from 1 upwards and x  represents the position of the electron. 

It is fairly straightforward to plot these functions for the first three levels as shown below, by taking values of x/ L from zero to one.

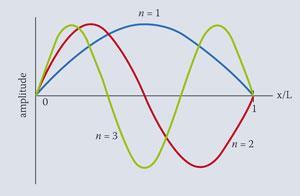
In this example the values of x/L would be given in radians, a clue to this being provided by the presence of the constant  in the above equation.

Paul Yates is an academic staff developer at Keele University, and is author of the book 'Chemical Calculations'.