Symmetry of buckminsterfullerene

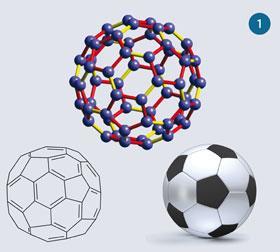
Buckminsterfullerene, C₆₀, is one member of the family of fullerenes, pure carbon molecules that are a cage of carbon atoms. These cages can be closed (buckyballs, fig 1) or open (buckytubes, fig 2). They were first reported in 1985¹ and were the subject of the Nobel prize for chemistry in 1996.² In the original experiment when graphite underwent laser ablation, C₆₀ was by far the most prevalent member of the fullerenes, with C₇₀ being the second most abundant.² C₆₀ contains 12 pentagons and 20 hexagons, fused such that the centres of the pentagons are at the corners of an icosahedron, making buckminsterfullerene a truncated icosahedron. Each of the pentagons shares its edges with adjacent hexagons. 

C₆₀ is the smallest buckyball in which none of the pentagons is in contact, ie shares an edge or a corner, with another pentagon. Its structure in three different representations is shown in fig 1, and may also be viewed interactively online.³

Euler's formula

In graphite hexagons fuse into a planar tessellation. It is the pentagons in C₆₀ that cause a bending of the shape out of the plane. Here we show that 12 pentagons are required to close the fullerene cage. We make use of Euler's formula, a characteristic of convex polyhedra: 

V - E  +F= 2                                      (1) 

where F  is the number of faces, V  is the number of vertices and E  is the number of edges. 

 

We can use it to help us solve simultaneous equations for a buckyball, ie a convex polyhedron composed solely of p  pentagons and h  hexagons as its faces. From this definition we can say straight away that: 

p  + h  = F                                        (2) 

Considering the vertices, it is evident that in any realistic structure a vertex will be shared between three faces. Since each pentagon has five vertices and each hexagon has six: 

5p  + 6h  = 3V                                  (3) 

Edges are shared between two faces. Therefore, counting edges: 

5p  + 6h  = 2E                                 (4) 

Using equations (2) to (4)  we can substitute for V, E  and F  in Euler's equation. Multiplying through by 6 to avoid fractions, gives: 

6(p  + h) + 2(5p  + 6h) - 3(5p  + 6h) = 12 

Multiplying out the terms, we see that the number of hexagons cancels, leaving us with p  = 12, which we were trying to show. 

We are assuming that the buckyballs are purely convex structures, ie structures without dents, where all the dihedral angles around edges are less than 180?. The fact that the number of hexagons cancels mean that closure of the carbon cage can be obtained with no hexagons (as in C₂₀) or with very large numbers of hexagons as is found in the largest buckyballs, eg C₁₀₀. 

Descartes' theorum

A net of a polyhedron consists of a planar set of edge-sharing polygons that can be folded along their edges to form the polyhedron. If a vertex is shared between three hexagons then the three hexagons are planar since the internal angle in a regular hexagon is 120° (the internal angle in a regular polygon is 

180° - 360° / n 

where n  is the number of sides of the polygon). 

In a buckyball such as C₆₀ or C₇₀, deviation away from the plane is achieved around a vertex that is shared between one pentagon and two hexagons. By considering these three polygons in a net we see that around the shared vertex the angles sum to 

108° + 120° + 120° = 348° 

This is 12° short of what is required for a planar arrangement. 

In constructing the polyhedron from the net this closure of the polygons across the 12° gap causes the vertex to move up into the third dimension. If we consider all five vertices of a pentagon surrounded by hexagons, this makes a total of 

5 × 12° = 60°

of angular defect whose closure causes curvature of the structure. The word 'curvature' is used loosely as deviation from the plane is actually in incremental steps, but considering that buckminsterfullerene is often loosely referred to as spherical, 'curvature' seems quite appropriate. In geometry, Descartes' theorem states that the total angular defect (where each defect is the shortfall from 360° in the net around a vertex) is 720° for a polyhedron that is homeomorphic (ie topologically equivalent) to a sphere. 

Since each pentagon contributes 60° of angular defect, the total number of pentagons required is 

720° / 60° = 12 

The equivalence of faces, vertices and edges

Vertices

One of the strongest pieces of evidence supporting the buckminsterfullerene structure at the time of its discovery was the carbon-13 nmr spectrum, which contains just one peak.⁴ This implies that all sixty carbon atoms in C₆₀ are in symmetrically equivalent, ie chemically equivalent, environments.   

The buckminsterfullerene structure is the only one that satisfies this condition along with chemical valency. It is also the largest buckyball for which this is true (the dodecahedral C₂₀ also contains just a single carbon environment). Each of the 60 carbon atoms is shared between a pentagon and two hexagons. 

Edges 

Brief inspection of the structure of C₆₀ reveals that there are two types of edge: edges shared between a pentagon and a hexagon, and edges shared between adjacent hexagons. Therefore we may not deduce from the carbon-13 nmr spectrum that all the C-C bonds are equivalent, even if all the carbon atoms are. 

Gas-phase electron diffraction studies⁵ have revealed that the pentagon-hexagon C-C bond lengths are 146 pm and the hexagon-hexagon C-C bond lengths are 140 pm. These relative lengths are consistent with the resonance form shown in fig 1, which ascribes multiple bond character to the hexagon-hexagon C-C bonds, and single bond character to the pentagon-hexagon C-C bonds. The fact that C-C single bonds average about 154 pm in length, with C=C double bonds about 134 pm long,⁶ shows that there is doubtless some delocalisation. 

Plugging p = 12 and h  =  20 into equation 4   we see that there are 90 edges altogether. Since in C₆₀ pentagons are never adjacent to other pentagons 

5 × 12 = 60 

of the edges must be of the pentagon-hexagon type. The remaining 30 edges must be of hexagon-hexagon type. 

One might consider there to be 

6 × 20 = 120 

hexagon edges, but 60 of these have already been taken into account as pentagon-hexagon edges. Since hexagons are in contact with other hexagons in C₆₀, the hexagon-hexagon edges are counted twice. 

Faces 

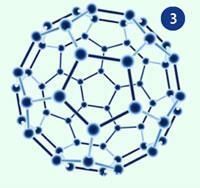
Given the icosahedral symmetry of C₆₀ we can look up the symmetry elements. These include six five-fold rotation axes that pass through the centres of opposite pairs of pentagonal faces. Combinations of rotations around these axes show that all 12 pentagonal faces are equivalent. Given that all the hexagons in C₆₀ are adjacent to pentagons it is easy to appreciate that combinations of rotations around the five-fold axes can also bring any hexagon to the position of any other hexagon in the structure, making all of the hexagonal faces equivalent. Fig 3  shows a buckyball viewed along a five-fold axis.

The pentagon isolation rule

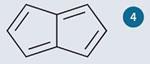
It has been observed empirically that stable buckyballs are those in which the pentagonal faces are isolated,⁷ ie not fused with other pentagons. C₆₀ is the simplest buckyball in which all 12 pentagons are isolated. One way to appreciate why this should be so is to consider the instability of pentalene (shown in fig 4), in which two cyclopentadiene units are fused together. 

Pentalene has eight ? electrons, which makes it anti-aromatic. It is so unstable that it was not until 1997 that it was successfully isolated and characterised.⁸

Resonance forms of C₆₀

To satisfy the valency of carbon in the resonance forms, each atom must be singly bonded to two other carbons and doubly bonded to a third. Therefore two thirds of the carbon-carbon bonds must be single and one third must be double in the resonance forms. 

We have seen that there are two types of carbon-carbon bond: 60 pentagon-hexagon and 30 hexagon-hexagon. Experimental data indicates that the hexagon-hexagon bonds are shorter than the pentagon-hexagon. 

The one resonance form that is consistent with these facts is that where the hexagon-hexagon bonds are double bonds and the pentagon-hexagon bonds are single bonds, as shown in the resonance form in fig 1. This is also consistent with anti-aromaticity considerations with cyclopentadienyl units. However, given the bond length data, there are obviously other resonance forms that need to be taken into account. In fact a great many resonance forms may be constructed by pushing curly arrows around the structure. It has been calculated⁹ that there are 12 500 resonance forms, but despite many of these being symmetrically equivalent, the number of different forms is still over a hundred.¹⁰

The second most stable buckyball: C₇₀

Equation 3  tells us that a 70-carbon buckyball with 12 pentagons must have 

(210 - 60)/6 = 25 

hexagons. The extra 5 hexagons go around an equatorial plane that defines, perpendicular to it, a unique five-fold axis through the buckyball (there were six five-fold axes through C₆₀ and no unique axis). 

This leaves the buckyball resembling a rugby ball in shape more than a soccer ball, and leaving it with D_5h symmetry. The structure is shown in fig 5  with the unique five-fold axis being horizontal. 

Planar graph structures

Some of the difficulties of analysing and comparing three-dimensional structures can be alleviated by considering planar graphs. In these structures the buckyballs are viewed down a five-fold axis, except the pentagon on the bottom face is expanded until is surrounds the rest of the structure with all the other polygons being displayed in the plane. The relative sizes and the shapes of the polygons are distorted but the structure remains topologically, ie graphically, accurate. The planar graph structures of C₆₀ and C₇₀ are shown in figs 6a & 6b. 

The twelve pentagons in these structures are found in two circular bands of five, leaving one in the centre and the final (bottom) one around the outside of the graph. 

The contrast between these two graphs shows us how the symmetry of these two buckyballs differs. While both graphs clearly display five-fold symmetry we can see that a line drawn from a corner on the outer pentagon to the centre of the C₇₀ graph passes through pentagons in both the internal groups of five. In the C₆₀ graph, such a line passes between two pentagons in the internal group of five closest to the centre. If a C₆₀ molecule is cut in half so that each half has an end pentagon and a band of five, the pentagons in the bands of five of each half of the molecule are related to each other by a rotation of 36? (a tenth of a complete rotation) about the axis that passes through the end pentagons. To obtain C₇₀ from C₆₀ one of these halves is rotated by 36? so that these pentagons line up. Where the pentagons line up there is a hexagon between them, preserving the pentagon isolation rule (discussed above). Between the pentagon-pairs there is space for two hexagons in the gap. Around the ring there are five of these gaps between the five pentagons; these extra five hexagons is what takes the hexagon count up to 25 for C₇₀.

Dual polyhedra

Two polyhedra are dual when the centres of the faces of one of them connect to make the corners of the other. As a result the number of faces and vertices are exchanged between pairs that are dual. In this way, the cube (6 faces, 8 corners) and octahedron (6 corners, 8 faces) are duals of one another. Similarly the dodecahedron (12 faces, 20 corners) and icosahedron (12 corners, 20 faces) are duals. The simplest buckyball, C₂₀, is a dodecahedron. Its planar graph structure is shown in fig 6c. 

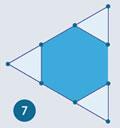
It is evident from the shape of the dodecahedron that connecting the centres of adjacent faces gives a 12-cornered polyhedron with 20 equilateral triangles for faces. It follows that truncating the corners such that one third of each edge is removed, leaves 20 regular hexagons in the place of the original 20 equilateral-triangle faces. This is shown in fig 7. 

The polyhedron resulting from such a truncation of the corners in an icosahedron is that of buckminsterfullerene.