Entropy – a masterclass

The classical definition

The classical thermodynamic definition of entropy is given in terms of the energy transferred reversibly as heat, dq_rev, to a system at a thermodynamic temperature T:

This definition refers to an infinitesimal change in entropy arising from an infinitesimal transfer of energy as heat. For an observable change that takes a system from an initial state i to a final state f, we add together (integrate) all such changes, allowing for the temperature to be different in each infinitesimal step:

If the change is isothermal (that is, with the system maintained at constant temperature; in practice, commonly by it being immersed in a water bath), then T may be taken outside the integral and (2) becomes:

where q_rev is the total energy transferred reversibly during the change of state. With energy (and, by implication, heat) in joules (J) and temperature in kelvins (K), the units of entropy are joules per kelvin (J K^-1).¹

Entropy is a state function; that is, it has a value that depends only upon the current state of the system and is independent of how that state was prepared. It is far from obvious that the definition in (1) implies that S is a state function, or equivalently that dS is an exact differential (one with a definite integral that is independent of the path of integration). It is commonly demonstrated that S is indeed a state function by using the Carnot cycle, as explained in textbooks.

The definition refers to the reversible transfer of energy as heat. A reversible process is one that changes direction when an external variable, such as pressure or temperature, is changed by an infinitesimal amount. In a reversible process, the system and its surroundings are in equilibrium. In a reversible expansion, the external pressure is matched to the changing pressure of the system at all stages of the expansion: there is mechanical equilibrium throughout. In reversible heating, the temperature of the external heater is matched to the changing temperature of the system at all stages of the heating: there is thermal equilibrium throughout. In practice, the external pressure or temperature needs to be infinitesimally different from that of the system to ensure the appropriate direction of change.

Three applications of the above expressions are as follows: 

In the first expression, n is the amount of gas molecules (units: mol) and R is the gas constant (units: J K^-1 mol^-1), which is defined in terms of Boltzmann's constant k (units: J K^-1) and Avogadro's constant N_A (units: mol^-1) by R = N_Ak. In the second expression the heat capacity C may be expressed in terms of the molar heat capacity C_m (units: J K^-1 mol^-1), as C = nC_m. If the pressure is constant during heating, use the isobaric heat capacity, the heat capacity at constant pressure, C_p. If the volume is constant, use the isochoric heat capacity, the heat capacity at constant volume, C_V. In the third expression, note the modern location of the subscript denoting the type of transition (Δ_trsX, not ΔX_trs). Moreover, the expression applies only to the change in entropy at the transition temperature, for only then is the transfer of energy as heat a reversible process. Enthalpies of transition, Δ_trsH, are molar quantities (units: J mol^-1, and typically kJ mol^-1), so an entropy of transition has the units joules per kelvin per mole (J K^-1 mol^-1).

The expressions in (4) apply to the system. Because the surroundings are so huge and of infinite heat capacity, any change taking place in the system results in a transfer of energy as heat to the surroundings that is effectively reversible and isothermal. Therefore, the change in entropy of the surroundings ΔS_surr is calculated from:

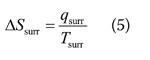
where q_surr is the energy transferred as heat into the surroundings. Note that 'rev' no longer appears, so this expression applies regardless of the nature of the change in the system (it applies to both reversible and irreversible processes).

Absolute entropies

The third law of thermodynamics is an assertion about the unattainability of absolute zero, but it implies that the entropies of all pure, perfectly crystalline substances are the same at T = 0.² It is then convenient ('convenient' in the absence of further information) to take that common value to be zero: S (0) = 0. The so-called 'absolute entropy' of a substance at any temperature, S(T), is then determined by measuring the heat capacity of a sample from as close to T = 0 as possible and up to the temperature of interest, and then using (2) in the form:

Various ways of extrapolating C(T) to T = 0 are available. If phase transitions occur before, ie below the temperature of interest, then (4c) is used and added to this expression. 

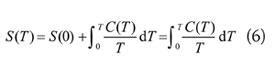
Tables of data commonly report 'standard molar entropies', S_m(T), at a stated temperature. The standard molar entropy of a substance is its molar entropy (units: J K^-1 mol^-1) when it is in its standard state at the specified temperature. The 'standard state' is the state for the pure substance at 1 bar (1 bar = 10⁵ Pa). Note that the use of 1 atm in this context is obsolete. The temperature is not a part of the definition of standard state: a standard state can be ascribed to any specified temperature. The 'conventional temperature' for tabulating data is 298.15K; it is a common error to include this temperature as part of the definition of a standard state.

The second law

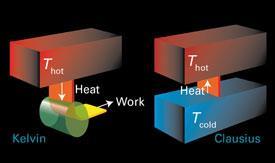
The second law of thermodynamics is a statement about the total entropy change, the sum of the changes in entropy of the system, ΔS_sys and its surroundings: ΔS_tot = ΔS + ΔS_surr. (It is common to drop the subscript sys and we shall do so.) Although there are several equivalent versions of the law, in terms of entropy a statement is:

The total entropy of an isolated system increases in any spontaneous change.

It is important to be precise about the meaning of 'an isolated system' in this statement. Here the isolated system consists of the actual system of interest (the 'system') and its surroundings. Such a composite system is isolated in the sense that there is no exchange of matter or energy with whatever lies outside it. In practice, the 'isolated system' of this statement might consist of a reaction vessel (the 'system') and a thermal bath (its surroundings). If the actual system of interest is itself isolated, in the sense that it does not exchange energy or matter with its surroundings, then the law applies to that system alone. In practice, such a system would consist of a sealed, thermally insulated reaction vessel.

A spontaneous change is one that has a tendency to occur without it being necessary to do work to bring it about. That is, for a spontaneous change in an isolated system, ΔS_tot > 0. As is well known but commonly forgotten, it is essential to consider the total entropy change: in many cases the entropy of the system actually decreases or remains the same in a spontaneous change, but the entropy of the surroundings increases and is responsible for the spontaneity of the change.

There is space to give one example. When a perfect gas expands isothermally, its change in entropy is given by (4a), regardless of whether or not the expansion is reversible: entropy is a state function, so the same change in S takes place independently of the path. We must, of course, use a reversible path to calculate the change, but the value we obtain then applies however the process actually takes place. For the change in entropy of the surroundings, there is no such restriction and we can use (5) for any type of process, reversible or irreversible. If the expansion is free (against zero external pressure), no work is done, and the internal energy is unchanged, so no energy is transferred as heat to or from the surroundings. Therefore, according to (5), the entropy change of the surroundings is zero and the total entropy change is equal to that of the system alone. That change is positive when V_f > V_i (because ln x > 0 when x > 1) and so free expansion is accompanied by an increase in total entropy. On the other hand, if the expansion is reversible, then work is done, a compensating quantity of energy as heat enters the system from the surroundings, the entropy of the surroundings falls, and overall the total change in entropy is zero.

Gibbs energy

Provided we are prepared to accept a constraint on the type of change we are considering, it is possible to avoid having to calculate two contributions to the change in total entropy. Thus, we introduce the Gibbs energy G = H – TS, colloquially the 'free energy', which is defined solely in terms of the properties of the system. For a system at constant temperature, ΔG = ΔH – TΔS. If, in addition, we also accept the condition of constant pressure, then it may be shown that ΔG = ΔH – TΔS_tot. Therefore, under these conditions, a spontaneous change is accompanied by a decrease in Gibbs energy of the system. Thus, if we are prepared to restrict our attention to processes at constant pressure and temperature, then we may perform all our calculations on the system. It should never be forgotten, however, that the criterion of spontaneous change in terms of the Gibbs energy is in fact a disguised form of the criterion in terms of the total entropy, and then subject to two constraints. The change in Helmholtz energy, ΔA = ΔU – TΔS, is the analogue when the volume rather than the pressure is held constant.

The statistical definition

The statistical definition of entropy is given by Boltzmann's formula:

where k is his constant and W is the weight of the most probable configuration of the system. Broadly speaking, the weight of a configuration is the number of distinguishable ways of distributing the molecules over the available states of the system, subject to the total energy having a specified value. That energy may, in general, be achieved with different configurations (all molecules in one state, for instance, or some in higher states and others in lower states, and so on). Boltzmann's formula uses the value of W corresponding to the most probable distribution of molecules over the available states. Thus, suppose a system consists of N molecules, then the weight of a configuration in which N₁ molecules occupy state 1, N₂ molecules occupy state 2, and so on, is

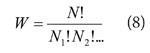
The value of W changes as the values of the N_i are changed. However, the N_i cannot all be changed arbitrarily because the total number of molecules (the sum of the N_i) is constant and the total energy (which is the sum of N_i E_i, where E_i is the energy of state i) is also constant. The N_i are varied, subject to these two constraints, until W attains its maximum value, and then that value of W is used in (7).

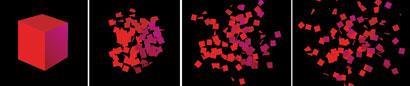
At T = 0, all the molecules are, of necessity, in the lowest state, so W = 1 and S = 0, in accord with the third law convention, but actually providing a value for the lowest entropy. As the temperature is increased, the molecules have access to a greater number of states, so W increases; thus the entropy of a substance also increases. There are other aspects of (7) that confirm that the entropy so defined is consistent with the entropy change defined in (1). In particular, note that, because W refers to the current state of the system, it is immediately clear that S as defined in (7) is a state function.

Boltzmann's formula provides a way of calculating absolute entropies from spectroscopic and structural data by using the techniques of statistical thermodynamics. It also enriches our understanding of entropy by providing insight into its molecular basis; we concentrate here on the latter aspect.

The presence of W in (7) is the basis of interpreting entropy as a measure of the 'disorder' of a system and of interpreting the second law in terms of a tendency of the universe to greater disorder. The term 'disorder', however, although an excellent intuitive guide in discussions of entropy (for instance, the standard molar entropy of a gas is greater than that of its condensed phases at the same temperature), must be interpreted with care.

At the simplest level, we can interpret the increase in entropy intuitively when a perfect gas expands isothermally (4a) as an increase in disorder on account of the greater volume that the molecules inhabit after expansion: it is less likely that the inspection of a small region will hold a molecule. Likewise, fusion (melting) and vaporisation both correspond to the loss of structure of the system, and so are accompanied by an increase in entropy, in accord with (4c) for endothermic processes. The increase in entropy with temperature, summarised by (4b), has already been dealt with: more energy levels become accessible as the temperature is raised.

In fact, that last remark is the key to the more sophisticated interpretation of W and hence S as a measure of 'disorder'. Imagine making a blind selection of a molecule from a system. The higher the temperature, the more states are accessible, so the probability of drawing a molecule from a particular state is lower.

How does this interpretation apply to the increase of entropy when a perfect gas undergoes isothermal expansion? The key is that the energy levels of a particle in a box become closer together as the volume of the box increases, so at a given temperature more states are accessible and the entropy is correspondingly higher. The relation between 'finding a molecule in a given location' and 'drawing a molecule from a given state' is far from obvious, and depends on an analysis, as Fermat said in another context, that is too long to fit into this margin.

Now we return to (1), and see how the statistical illuminates the classical. The analogy I like to use is that of sneezing in a busy street (an environment analogous with high temperature, with a great deal of thermal motion already present) and sneezing in a quiet library (an environment analogous with low temperature, with little thermal motion present). A given sneeze (a given transfer of energy as heat) contributes little to the disorder already present when the temperature is high, and so the increase in entropy is small, in accord with (1). However, the same sneeze in a quiet library contributes significantly to the disorder, and so the increase in entropy is large, also in accord with (1).

Conclusion

The definition of entropy in (1) might seem abstract, but is illuminated by the statistical interpretation. The concept of entropy in terms of a measure of disorder is a highly intuitive matter, and provided it is understood that the total entropy is the discriminant of spontaneous change, then it can be appreciated that locally structures can emerge as the universe sinks ever more into disorder. The crucial point, however, is that numbers may be attached to disorder, and this compelling qualitative concept rendered quantitative.

Until his retirement in 2007 Peter Atkins was professor of chemistry at the University of Oxford and fellow and tutor of Lincoln College.

Notes

1. All units derived from the names of people are lower case; their symbols have an upper case initial letter.
2. Note that we write T = 0, not T = 0K (just as for mass we write m = 0, not m = 0kg): the thermodynamic temperature is absolute and zero is its lowest value regardless of the scale.

Further Reading

I apologise that my references are to my own writing. In them, will be found justifications of the statements and equations presented in this presentation. Others, of course, have provided fascinating insights.

• A very short introduction: to the Laws of Thermodynamics. Peter Atkins, Oxford University Press (2010). This short account originally appeared as Four Laws that Drive the Universe  (2008).
• Elements of Physical Chemistry. Peter Atkins and Julio de Paula, Oxford University Press and W.H. Freeman & Co. (2009).
• Physical Chemistry. Peter Atkins and Julio de Paula, Oxford University Press and W.H. Freeman & Co. (2010).
• Quanta, Molecules, and Change. Peter Atkins, Julio de Paula, and Ronald Friedman, Oxford University Press and W.H. Freeman & Co. (2009).
• Chemical Principles. Peter Atkins and Loretta Jones, W.H. Freeman & Co. (2010).