The power of NMR: in two and three dimensions

The success of one dimensional, high-resolution NMR stems from the unique insights that it can provide about molecular structure.¹ The chemical shift of a nucleus gives invaluable information about the chemical environment in which that nucleus is located. Coupling interactions between hydrogen nuclei, as revealed by characteristic splitting patterns in the ¹H-nmr spectrum, provide information about the location of one group of hydrogen atoms relative to others in the molecule. And the nuclear Overhauser effect (nOe) can shed light on molecular stereochemistry.  

The concept of two dimensional NMR spectroscopy was first put forward in 1971 by Belgian scientist Jean Jeener, working at the Université Libre de Bruxelles.² The principles behind this technique evolved naturally from the pulsed-Fourier transform (FT) experiment, but what benefits has this technique brought?^3,4 

Two dimensional NMR  

In the one dimensional pulsed-FT experiment, a spinning nucleus is placed in a magnetic field; it is then excited from a lower energy state to a higher state by a pulse of radiofrequency radiation. This pulse generates a simultaneous response from all the different resonances which are present in the molecule, and these responses must then be disentangled from one another, by a Fourier transformation, to produce an nmr spectrum.  

In the corresponding two dimensional NMR experiments, excitation is achieved by a sequence of two or more pulses. In addition, there is one (or more) variable delay period between these pulses. To generate the second dimension, this pulse sequence is repeated many times, and the length of the variable delay is increased each time. After Fourier transformation, we obtain a dataset which consists of a series of one dimensional nmr spectra. Each spectrum differs subtly from its predecessor, as a result of changes which have occurred during the incremental delay.  

By applying a second Fourier transformation to the dataset, along the 'axis' of the variable delay, and therefore orthogonal to the first transformation, we obtain the two dimensional nmr spectrum. This spectrum retains the chemical shift information of the one dimensional nmr spectrum along the horizontal axis (obtained from the first Fourier transformation) as well as providing new information about a second nmr parameter in the vertical dimension (the new dimension 'reports' solely on whatever kind of 'evolution' has occurred during the incremental delay as revealed by the second Fourier transformation). The strength of two dimensional NMR spectroscopy is its ability to provide 'correlations' between any two sets of nmr parameters, enabling couplings or nOes to be established in a more efficient or less ambiguous way than was previously possible.  

COSY for chemists 

Hundreds of two dimensional NMR experiments have been described over the past 20 years, all of which are designed around the same basic principles: ie all contain multiple pulses and at least one variable inter-pulse delay. However, only a handful of these techniques have stood the test of time and continue to find routine application today.  

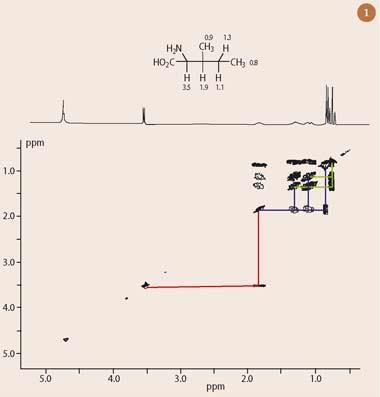
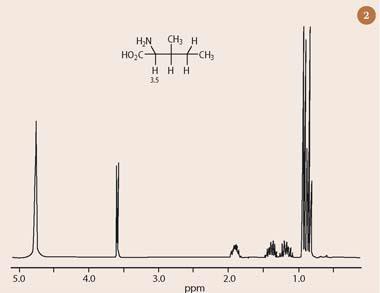
The most commonly-encountered modern two dimensional NMR technique is homonuclear shift-correlation spectroscopy (COSY), which presents ¹H chemical shift data on both the horizontal and vertical axes. The COSY experiment establishes 'connections' between protons via their mutual couplings, as shown in Fig 1 (the two dimensional COSY spectrum of the amino acid, isoleucine). The most easily attributable hydrogen resonance in the one dimensional ¹H-nmr spectrum of isoleucine (Fig 2) is the γ-proton at 3.5 ppm.¹ This proton has a characteristic chemical shift, owing to the substitution of a nitrogen atom at the methine carbon (protons attached to a carbon bearing such an electronegative atom have a predictable chemical shift in the 3-5 ppm range).  

As expected, the γ-proton in Fig 2 is also split into two peaks, as a result of coupling to the single proton in the neighbouring CH group (explained by the 'n+1' rule ).¹ However, it is not immediately obvious which peak in the one dimensional ¹H-nmr spectrum of isoleucine corresponds to this CH neighbour, nor is it trivial to continue the analysis of this spectrum any further past this point in the molecule. 

Fortunately, the two dimensional ¹H-¹H COSY spectrum of isoleucine provides direct answers to these questions, without requiring a lengthy analysis of all the complex splitting patterns presented by the remaining protons in the rest of the molecule. To interpret the two dimensional nmr spectrum (Fig 1), first draw a line horizontally, starting from the γ-proton of isoleucine, which resonates at 3.5 ppm in both dimensions of the 'diagonal' (running from bottom left to top right). This line intersects an 'off-diagonal' peak at 1.9 ppm (red lines), thus revealing this to be the chemical shift of the adjacent methine hydrogen (which is coupled to the α-proton through three bonds). The same process can be repeated twice more to assign all the other proton chemical shifts in isoleucine.  

Thus, if a second line is drawn horizontally, this time starting from the diagonal at 1.9 ppm, a further three 'connections' are revealed to adjacent protons at 1.3, 1.1 and 0.9 ppm (blue lines). The protons at 0.9 ppm correspond to the attached methyl group, which is a doublet. The protons at 1.3 and 1.1 ppm are associated with the next CH₂ in the chain. Both of these protons share further couplings with the second methyl group at the end of the chain (a triplet centred at 0.8 ppm), as indicated by the green lines in Fig 1. This then completes the 'connection' of all the hydrogen atoms in isoleucine - without reference to splitting patterns or chemical shift. 

Other two dimensional experiments 

Other useful two dimensional NMR experiments include the family of heteronuclear correlation experiments: ¹³C-¹H COSY, HSQC, HMQC and HMBC. All of these connect the chemical shifts of two different nuclei (most commonly ¹³C and ¹H), which are represented on separate axes of the two dimensional plot.  

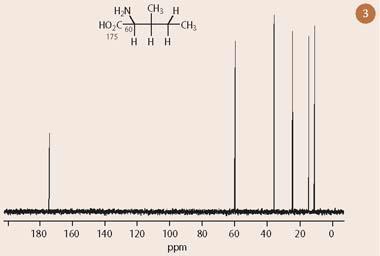
Figure 3 shows the one dimensional ¹³C-nmr spectrum of isoleucine, which presents six resonances, one for each carbon. Figure 4 illustrates the corresponding ¹³C-¹H COSY spectrum with the one dimensional ¹³C-nmr spectrum superimposed on the horizontal axis and a one dimensional ¹H-nmr spectrum projected along the vertical axis. (Note that the carbon peak at 175 ppm, corresponding to the carboxylic acid group, has not been included in the plot because it has no hydrogens directly attached.)  

As for the homonuclear proton-proton COSY experiment, the analysis of a heteronuclear correlation experiment is a straightforward matter, requiring horizontal and vertical lines to be drawn to 'connect' together ¹³C and ¹H resonances. Thus, moving horizontally across the ¹³C-¹H COSY spectrum at a proton chemical shift of 3.5 ppm leads to an intersection with a peak located at 60 ppm in the 'second' (¹³C) dimension, as shown by the red lines in Figure 4. Because this experiment has been set up to detect carbons and protons which are connected to one another by a single bond, the interpretation of this two dimensional nmr correlation is that the resonance appearing at 60 ppm in the ¹³C-nmr spectrum must correspond to the α-carbon.  

Admittedly, we might have predicted this assignment, based on the knowledge that the chemical shift of a functional group in ¹³C-nmr is roughly 20 times the corresponding ¹H chemical shift. However, it would be difficult to assign conclusively any of the remaining four carbon resonances in Figure 4 by looking at the one dimensional ¹³C-nmr spectrum alone.  

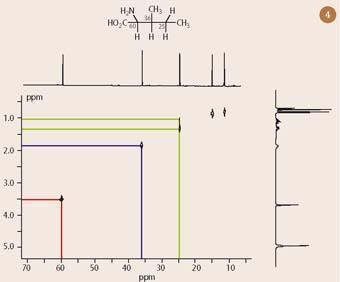
Since all the proton assignments for isoleucine are already known from analysis of the ¹H-¹H COSY spectrum (Fig 1), it is relatively easy to assign each of these carbon resonances, based on the known chemical shifts of the attached hydrogens. Thus, the blue lines in Fig 4 identify the carbon at 36 ppm as belonging to the next CH in the chain - because it is bonded to the hydrogen at 1.9 ppm. Similarly, the green lines show that the carbon at 25 ppm is bonded to two hydrogens at 1.1 and 1.3 ppm, thereby proving this to be the next CH₂  in the chain. (I leave the ¹³C assignments of the remaining two methyl groups, at 11 and 15 ppm for the reader.) 

The third two dimensional NMR experiment to find routine use in solving the structure of organic compounds is nuclear Overhauser enhancement spectroscopy (NOESY). This technique measures nuclear Overhauser enhancements (nOes) for protons which are spatially close to one another in a format which appears superficially similar to that of COSY. 

However, the pattern of off-diagonal peaks in the NOESY experiment provides information about the arrangement of hydrogen atoms in space, rather than the pattern of their covalent bonding. When NOESY is used in conjunction with the foregoing two dimensional NMR experiments, it is often possible to obtain enough information and constraints about the relationships between all the ¹H and ¹³C nuclei in a molecule of unknown structure, so that only one molecular structure is logically permissible. 

Protein NMR spectroscopy in three dimensions 

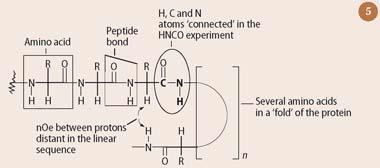
A protein is a linear polymer of amino acids (eg isoleucine) which are joined together by peptide bonds (see Fig 5). Proteins are typically several orders of magnitude larger than the small organic molecules for which the original two dimensional NMR experiments were designed. However, proteins are constructed from the same elements as small organic molecules: primarily, hydrogen, carbon, nitrogen and oxygen, so the same nmr theory applies.  

The main difficulty in analysing the one dimensional ¹H-nmr spectrum of a protein is that it contains a very large number of peaks crowded into a narrow chemical shift range between 0-10 ppm. This inevitably results in a high degree of accidental peak overlap. As a result, it is necessary to apply multidimensional NMR techniques (two-, three- and even four-dimensions) to the study of proteins. The higher dimensions effectively 'spread' these congested resonances out over a much larger area (for two dimensional NMR), or volume (for three dimensional NMR) - thereby drastically reducing the probability of accidental peak overlap. 

Kurt Wüthrich was the first person to solve a protein structure by NMR in 1984.⁵ He used the same two dimensional NMR techniques which had been developed previously for small organic molecules by fellow Swiss scientist, Richard Ernst,³ who was awarded the Nobel prize for chemistry in 1992 for his work in this area. (In 2002, Wüthrich was also awarded the Nobel prize in chemistry for his achievements in developing NMR for the study of proteins.)  

Wüthrich first assigned each resonance in the ¹H-nmr spectrum of the protein BPTI to a specific hydrogen nucleus, using experiments such as COSY, which established 'connections' between protons made through covalent bonds. He then determined the overall three dimensional structure of the protein by making use of correlations observed in a NOESY experiment. Because the nuclear Overhauser effect probes 'connections through space', rather than through bonds, it identifies protons which are brought into close proximity to one another by virtue of the folding of the protein, even though these protons may be quite distant in the linear sequence (see Fig 5). Given sufficient nOe-derived 'distance constraints', it then became possible to reconstruct the three dimensional shape of the BPTI protein. This reconstruction generally requires the use of computers, which convert the large number of nOe-derived distance restraints into energy terms, and then minimise the energy of the system as a whole. Such an approach typically results in an ensemble of structures, depending on which initial conditions are used by the computer algorithm. These structures overlap in highly ordered regions of the interior of the BPTI protein, but there is less convergence in more disordered regions on the surface. 

Protein NMR spectroscopy has evolved rapidly since Wüthrich's first experiments more than two decades ago. Nowadays, it is common practice to study proteins which have been isotopically-labelled,* subjecting them to a variety of three dimensional multinuclear NMR experiments.  

The modern strategy for solving the structure of a protein by NMR begins with the NH protons in the peptide bond (Fig 5). For a reasonable sized protein many NH resonances will be crowded into a narrow region of the one dimensional ¹H-nmr spectrum between 6-10 ppm, and there will inevitably be a high degree of overlap. However, the probability of overlap is greatly reduced by the introduction of not just a second, but also a third dimension.  

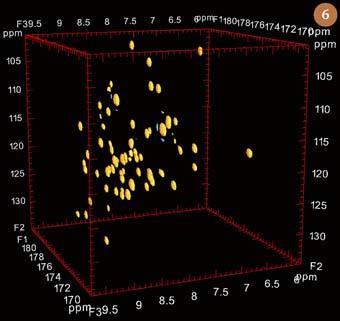
In the case of the three dimens-ional NMR 'HNCO' experiment these two extra dimensions correspond to the chemical shift of the nitrogen atom to which this hydrogen is attached (labelled by ¹⁵N), and to that of the adjacent C=O group in the peptide bond (labelled by ¹³C). As well as serving to reduce the probability of overlap for NH protons, this experiment also 'connects together' all the proton, nitrogen and carbon resonances in a peptide bond. Thus, each of the various peptide bonds in a protein appears individually as a small sphere in the HNCO experiment shown in Fig 6. The limits of this experiment are set by a cube which is defined by three orthogonal axes corresponding to the chemical shifts of mutually-coupled ¹H, ¹⁵N and ¹³C nuclei. Many other three dimensional NMR experiments have been developed for the study of proteins over the past two decades. However, only a few of these, such as HNCA and HN(CO)CA, which when used together with HCNO allow the assignment of all the carbon, hydrogen and nitrogen resonances in the backbone of a protein, continue to find routine use.  

The future of protein NMR 

In spite of the massive advances which have been made over the past 20 years, the task of comprehensively assigning all the ¹H signals in a reasonably-sized protein remains a daunting one. For this and other reasons, NMR continues to be limited to the study of proteins which are, at least by biological standards, relatively small (most are below 30 000 atomic mass units). In this sense, NMR is at a disadvantage when compared with X-ray crystallography, the other important technique for determining the three dimensional structure of proteins, since there is no general limit with respect to molecular size for X-ray crystallography. This is reflected by the number of protein structures which have been solved by these two techniques: currently around 35 000 for X-ray crystallography, as against 5000 for NMR.  

However, NMR does enjoy some advantages. For example, NMR can solve the solution structure of proteins which are difficult to crystallise, as is often the case for membrane proteins. NMR can also provide a wealth of information about internal motions in the physiologically-relevant solution state, which are not available from a crystal structure. Wüthrich has commented that we currently lack a functional interpretation for much of the dynamic information which is being revealed by NMR studies of proteins, and that such data could, perhaps, provide novel insights into the function of proteins in the future.⁵ 

Dr Geoff Brown is lecturer in NMR spectroscopy in the department of chemistry at the University of Reading, PO Box 224, Whiteknights, Reading RG6 6AD.