Simplify the maths in chemistry with the Singapore bar model

Galileo claimed that you can’t understand how the world works until you understand the maths. Mathematics, and algebra in particular, has become our key to understanding science. If you can’t do the maths, the lock stays locked.

Chemistry in particular is unforgiving. Unlike simple physics and biology, the simplest relationships and models of chemistry require multiple variables. You can learn simple chemical phenomena without mathematics, but you can’t understand them.

Algebra is a key to unlock chemical ideas, but if you are struggling with the maths, you won’t have enough working memory to understand the chemistry.

Fortunately, there is a way to reduce the conceptual difficulty of algebra – you can represent the numbers pictorially. Instead of a + b = c, you can use bars.

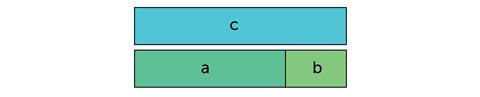
This may not look like much of an improvement (especially if you can’t remember finding a + b = c tricky), but making the relationship visible frees up your working memory to do the real business: understanding chemical relationships.

The bar-model approach was developed in the 1980s by Singapore’s Ministry of Education to help pupils develop problem-solving skills in mathematics. The rapid rise in mathematical performance of the country’s school children brought Singapore maths and the bar model to much wider attention. There is a good chance your students have learned how to use the bar model to solve algebraic problems already.

The theory underpinning bar model is known as CPA: first concrete, then pictorial and finally abstract. As science teachers we usually go straight to abstract – algebra. But many of our learners haven’t mastered the abstract algebra sufficiently for it to be a useful tool. Is it possible to go back a step and still teach the chemistry? Not always, but when the bar model is appropriate, it can significantly reduce the cognitive load of problem solving.

Bar modelling in chemistry works particularly well for conservation relationships. In the rest of this article I will demonstrate how you can use them for conservation of mass in reactions, conservation of energy and conservation of charge.

Conservation of mass

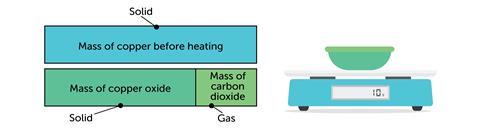
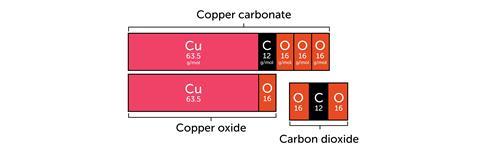
You represent quantities with bars instead of letters. For example, when you heat copper carbonate, thermal decomposition occurs. The mass of material seems to decrease. We might explain it in words:

The mass seems to have decreased, but really the missing mass is carbon dioxide.

Or we might explain it as algebra:

Mass of copper carbonate before heating = mass of copper oxide + mass of carbon dioxide.

Or even:

m_CuCO₃ = m_CuO + m_CO₂

You’ll leave lots of learners behind. There is too much going on. A bar model reduces this load by making the relationship pictorial:

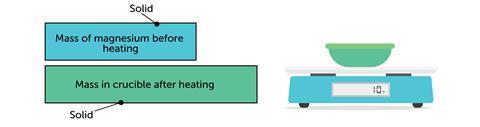
The bar model works the other way around. For example when magnesium reacts with oxygen:

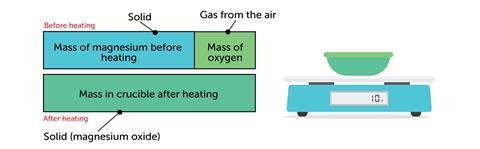
Representing the mass of the gas as a bar turns an abstract idea (gas has mass) into something more concrete – something you can point to, measure and calculate with.

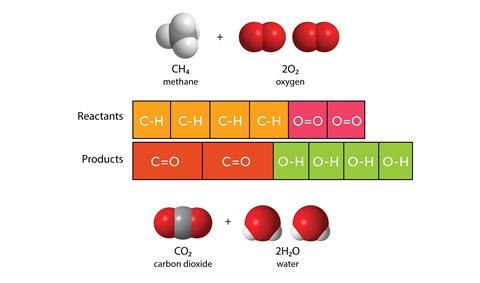
You don’t need to stop at this stage. Bar models can be used later on when learning about conservation of mass with symbol equations:

Conservation of charge

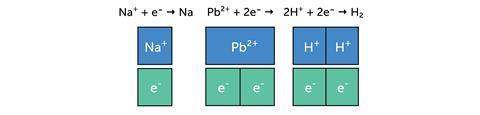
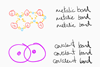
The next example uses the bar model to represent the charges in ionic compounds.

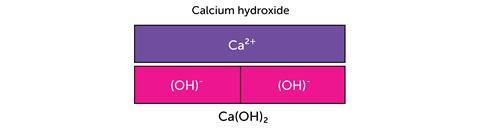
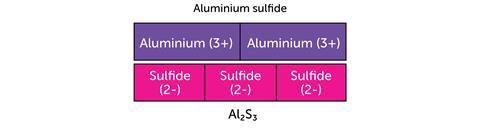
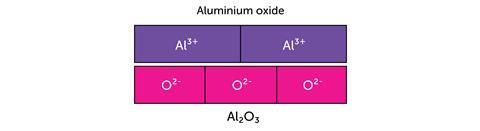
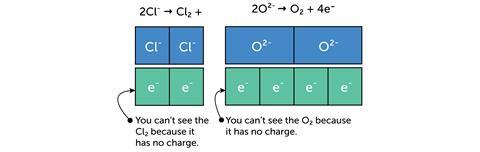
The bar model can be used in the same way when balancing ionic half equations:

Conservation of energy

The final abstract quantity I’m using bar models to represent is energy. The diagram below uses the bars to represent the bond energies in a reaction. In this case the difference between the lengths of the bars represents the energy change that accompanies the reaction:

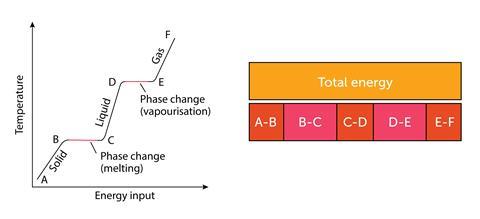
Students often find combining latent heat and specific heat difficult – a bar model can make the abstract pictorial:

The great advantage of bar modelling is that it doesn’t replace algebra: it is a visual representation of algebra. Some students will only need to be shown how the bar model works once in each context and get the idea. Others will find them helpful for longer. Whenever I teach a new concept that the bar model can support, I put it in the corner of the slide and use it in my initial explanation – it helps to be able to point to abstract concepts. I often leave it on subsequent slides when my students are practising, so I can refer to it if anyone gets stuck.

In short, reducing the extraneous cognitive load by using a bar model leads to more learning.