Improve numeracy for all

It’s impossible to remove the numeracy from science. Whether you’re plotting graphs of rates of reaction, calculating yields or even just using a thermometer, numeracy is an integral part of our subject. It’s also seen as socially acceptable to struggle with numeracy in a way that doesn’t apply for literacy. This means we have to work really hard as science teachers to push the development of these skills.

Many students struggle with numeracy as part of a wider range of special or additional needs, while other students may only experience difficulty with the maths. Unfortunately, there’s no magic bullet to remove these difficulties, but there are strategies beyond the obvious of rote learning and repetition of content that can help.

Consider the vocabulary you use

The language of maths can be confusing for learners of all ages. Before students can answer a question they need to understand what is being asked. The Association for Science Education has produced an open access document to help educators get to grips with this issue before tackling it in the classroom.

Science teachers should define the necessary vocabulary (ideally using the same words as the exam boards), rehearse it and get students to use and repeat the words in context. Start simple – ‘big’, ‘medium-sized’ – and build up to more complicated ideas like types of correlation and anomalous results. A numeracy placemat could also help as a reference resource for some learners.

Rethink teaching methods

Think about how you group your learners. Cooling curves used to be the bane of my life – some lessons would be spent just whizzing around helping students read thermometers. I then regrouped the learners so each pair had someone who was confident at reading a thermometer. I asked the students to work together so those students skilled at scale reading could teach those who hadn’t yet mastered it. This strategy transfers to other topics where numeracy is used and I’ve found that students teaching other students is a very powerful learning aid for both those explaining as well as those on the receiving end. Try to avoid using numbers with decimal places until students have a good grasp of this concept.

One of the most simple strategies is to break down calculations into smaller, manageable steps. You can either scaffold the calculation – break the steps down using something like a flow chart – or get students to complete new problems alongside a worked example so they can remember the steps and have a model to follow. Completing these tasks on a mini whiteboard may help those with low self-confidence – they can rub out mistakes before committing them to paper.

Some learners respond better to tactile strategies because they can visualise quantities. One of my favourite classroom strategies was balancing chemical equations using Skittles on a whiteboard. Students must have the same number of Skittles at the end as at the start, and this strategy helps them to both visualise what’s happening to the atoms and write a balanced equation. Using liquids in containers with different measures can also help students convert between units because they can see the volumes for themselves.

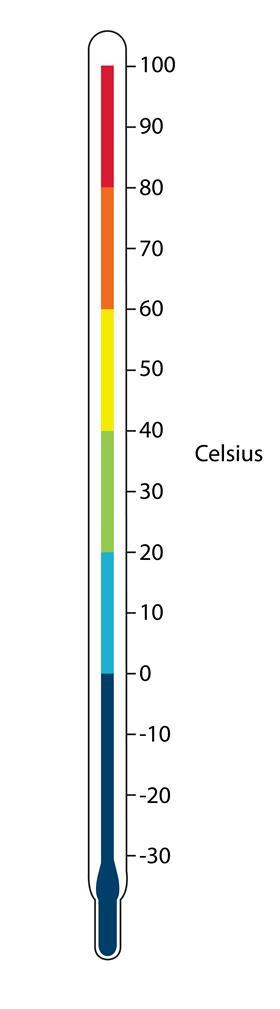
A similar strategy to help learners is to capture results using coloured scales, such as a diagram of a thermometer. Using this method, students who can’t visualise the magnitude of relative quantities can begin to make meaningful comparisons in the same way as reading a graph.

Students with numeracy difficulties can find graphs challenging – not necessarily reading the trends from a graph, although this is a skill that needs to be rehearsed, but plotting data on axes. If you have access to technology in your classroom, then start by creating Excel templates, ensuring students can only type in the required cells so they can’t delete anything important. Once students become comfortable graphing in Excel, you can switch to teacher-created axes and build up to students making up their own.

It’s more powerful to teach for understanding than to teach the methods required to complete particular calculations, as students are more likely to spot errors in their results. If students understand the concepts involved, they will probably notice that they have substituted the wrong numbers in their equation or used the wrong operator, for example. Understanding rate of reaction and then exploring different scenarios before moving on to the calculations is likely to be far more effective than jumping straight into the maths.

Finally, relate the maths in science to real life. As science teachers, we have the advantage that all our maths is applied, and this can help with the retention of knowledge and engagement of those students who find numeracy a challenge.