Nine tips for scaffolding multi-step calculations

Students often have difficulty sequencing longer maths tasks. They struggle to retain information in their working memory to maintain the thread of longer, multi-step calculations. The recent increases in mathematical demand in some science curriculums has increased this challenge for many students.

Tricky maths problems become more of a problem for students under stress, as the amount of information a student can hold in working memory decreases. These issues are multiplied if the student has maths anxiety or is working under test conditions or in a noisy classroom.

Exam questions without scaffolding can present particular problems for students with dyslexia and other specific learning differences (SpLD). We tend to think of dyslexia as a problem with spelling and reading. While sometimes true, dyslexia also has an impact on maths. Students with SpLD may have strong non-verbal reasoning, but find it difficult to articulate their thinking.

Interventions shown to help students with SpLDs, such as dyslexia, dyspraxia and dyscalculia, often help other students as well. So, whether or not you teach students with SpLDs, these strategies for helping students sequence steps and articulate their thinking are worth following.

Build up the basics

Students need to carry out each separate step fairly automatically for success in multi-step calculations. Ensure students have the following maths skills before applying them to a multi-step problem.

1. Handling units

Students should include units throughout a calculation. This is important for two reasons. Firstly, it is more obvious if they need to convert units. For example, if a concentration is given in g dm^-3 but a volume is given in cm³ the volume should be converted to dm³ before substituting into the formula. Secondly, it’s a useful way of checking for errors. If students end up with the units for concentration as dm³ g^-1, they know they’ve made a mistake.

Additionally, more familiarity with units means students know which units are used for each type of measurement (eg dm³ for volume, g for mass), and recognise that something measured in dm³ relates to a volume.

2. Making sense of formulas

Understanding that concentration is how much solute is present in a certain volume of liquid helps to make sense of the formula, because the formula represents, in words, the amount per volume. Something concentrated has a large amount in a relatively small volume.

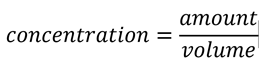
Ensure students also grasp that, for example, the molar mass is the mass per mole of a substance. So, a very large atom or molecule will have a large molar mass because each atom or molecule is bigger.

3. Speaking the language

Encouraging students to talk through what they are doing in a calculation helps them embed the appropriate language. For example, it helps them make the link between ‘per’ and ‘divide’.

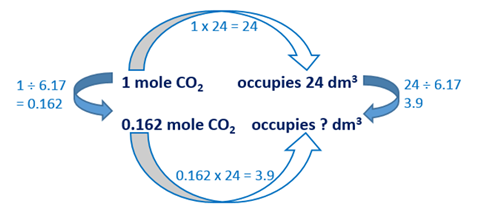
4. Using ratio and proportion

Students often need help setting out answers to questions involving ratio and proportion. For example, if we know that 1 mole of CO₂ gas occupies 24 dm³, what volume would 0.162 mole of CO₂ gas occupy?

Encourage students to think through this calculation. We have a ratio of 1 mole CO₂ to 24 dm³ volume. To get from 1 to 24 we multiply by 24. So to work out the volume for 0.162 mole CO₂, we multiply 0.162 by 24 to get 3.9 dm³.

Scaffold it together

Once students are comfortable with calculation basics, model the process for solving a multi-step calculation.

5. Provide the narrative

First, describe what the question tells you and what it asks you to do.

For the example problem above, you might say, ‘The balanced chemical equation tells me one mole of copper carbonate gives me one mole of copper chloride. Moles are our currency in chemistry. I know the mass of copper chloride. So, I first have to work out the number of moles that corresponds to. Once I know this, I can say how many moles of copper carbonate would be required, and then I can convert that into grams to get the answer.’

6. Signpost steps

Write signposts that describe what is done at each step.

7. Colour code

Colour helps students make connections between the different parts of the chemical equation and the calculations. People with SpLDs who are good at making connections can still find links become obscured when buried within a lot of text.

8. Put equations before numbers

Present the equation needed before substituting numbers to do the calculation.

9. Format carefully

Avoid visual stress by setting out working in plenty of white space. Set fractions out visually as a over b, not inline as a / b. Most word processors have an ‘Insert equation’ function.

Vary on a theme

While this sort of scaffolding is useful for introducing multi-step calculations, it becomes more powerful when you vary questions. For example, we could be given the mass of the starting material and need to calculate the mass of the product.

Ask students what other ways the question could be asked – ie how much HCl is required or how much CO₂ is produced? Then get students to write their own scaffolded answer. Giving students information and asking them what they can find out from it is known as ‘goal-free problems’ in maths education.