Investigating Crystal Structures

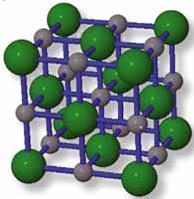
If we consider sodium chloride, given the high symmetry of the lattice we would expect some kind of order to the terms in the structure, or Madelung constant, but it isn't obvious what that order is at first. Figure 1 shows a fragment of the sodium chloride crystal structure: grey ions represent sodium, and green chloride; the ions are only shown at half-radius size to show the structure more clearly; blue lines connect ions that are, in reality, touching. This fragment is known as a unit cell because the bulk crystal structure can be obtained by displacing the cube, or by stacking together identical cubes. If we count the ions, starting from the neighbours of the central sodium ion, we find that patterns emerge:  

Having now considered all the ions in the cubic fragment, we need to visualise neighbouring cubes to progress further.

The number of ions at distances r√4, r√5, and r√6 from the central sodium ion can be seen using Fig 2, bearing in mind that the central cube has six of these neighbouring face-sharing cubes. A couple of patterns emerge: the sign of the ions alternate as we move to more and more distant neighbours, which is what is expected given that ions tend to be in contact with oppositely charged neighbours. Also we see that the distance of the ions has followed the pattern r√x where x is the number of ions away an ion is from the reference ion. However, complications arise if we try to continue this trend for distances much further out.  

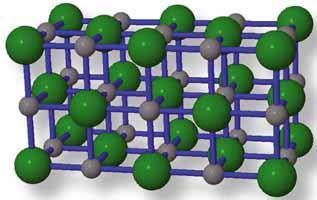
Consider, for example, a large cube of three cubes by three cubes by three cubes, totalling 27 cubes. The central cube is in contact with 26 neighbouring cubes. Six of these share a face with the central cube's six faces;12 of these share an edge with the central cube's 12 edges; and eight of these share a corner with the central cube's eight corners. Now consider some of the more distant ions in terms of these neighbouring cubes.

For the seven-away neighbours we need to consider the cubes diagonally opposite the 12 edges of the central cube. The seven-away neighbours are in the centre of these 12 cubes. These curiously also have the same charge as the reference ion because they too are in the centre of a unit cell. According to Pythagoras, the distance of these ions from the central ion is not r√7 but r√(2² + 2²) = r√8.

We meet another surprising result when we consider the eight-away neighbours. There are two seemingly unequal sets of ions that are an equal distance from the reference ion. One of these is made up of ions that are one 'step' of r away from the seven-away numbers in a direction perpendicular to the crystal plane holding the central reference ion and the seven-away neighbours. Since there are 12 of these seven-away neighbours there must be 24 ions comprising this set of eight-away neighbours. This is because they are displaced a distance r from the seven-away neighbours in both perpendicular directions from the crystal plane. These ions are of opposite charge to the reference ion and are a distance of r√(2² + 2² + 1²) = r√9 away. The other set of eight-away neighbours comprises those ions that are three steps of r away along any of the crystalline axes since r√9 = 3r. These are the ions in the six adjacent face-sharing cubes that are in the centre of the face opposite the face that is shared with the reference cube. So there are six of these ions and they are also of opposite charge to the reference ion.

The Madelung series

The series we have obtained so far is:

A = 6/√1 - 12/√2 + 8/√3 - 6/√4 + 24/√5 - 24/√6 - 12/√8 + (24 + 6)/√9

where a plus sign indicates an attractive interaction and a minus sign a repulsive interaction. How can we predict 

subsequent terms? Let us consider the denominators first. These terms are the result of the Pythagorean expression r√(x² +y² + z²) where x, y and z are the number of steps of r along each of these axes in the crystal. The lack of a √7 denominator is because it is impossible to arrive at seven from the sum of the squares of three integers, while there are two terms with a √9 denominator because there are two ways of constructing nine from the sum of the squares of three integers: 9 = 2² + 2² + 1² = 3² + 0² + 0². For each term the numerator effectively gives the number of combinations of x, y and z that give the denominator value, bearing in mind that x, y and z may be positive or negative, corresponding to the direction of stepping along the crystal axis. With each step of r along a crystal axis the charge of the ion changes sign. Therefore when the sum x + y + z  is  positive it corresponds to a repulsive interaction and a negative term in the series. We can generalise in this way because moving any number of integer steps of ralong any of the crystalline axes from an ion takes us to another ion. It is not so simple in other types of crystal structure.

From this general description of the Madelung series, it is possible to automate the calculation of the different terms. Taking the approach of the n-away neighbours, ie considering ions a given distance from the reference ion, we first need to consider if there is more than one set of x, y  and z  that equate to that distance, or indeed none at all. For example, there are two sets of ions giving rising to √18 in their denominators, because 18 = 4² + 1² + 1² = 3² + 3² + 0², while there are no ions a distance r√15 from the reference ion.

Given these derived values of x, y and z, the number of combinations of them depends both on whether they are non-zero and how many are different. There are 3!/m! different combinations of the x, y and z where m is the greatest number of times a value appears in the sequence. Non-zero terms can take positive or negative values depending on whether the ion being counted lies along the positive or negative axis, so there are 2ⁿ  combinations depending on these signs where n is the number of non-zero values of x, y and z. So the numerator for each r√(x² + y² + z²) denominator is 3!/m! × 2ⁿ. The maximum multiplicity of a set of  x, y, z  is when all three values are different and non-zero, the first of these occurring at r√(1² + 2² + 3²) = 14 when there are 2³ × 3! = 48 combinations. 

Convergence problems

By considering terms with gradually increasing denominators we are effectively considering concentric spheres of ions with reference to our central ion. As such the series will consist mainly of alternating positive and negative ions, and therefore will never converge. So even when the algebraic problem is understood there still remains a computational one. The convergence problem can be overcome when considering concentric cubes rather than concentric spheres of ions. Ions lie in concentric cubes that are defined by the largest (in magnitude) value of the x, y and z values that define their position from the reference ion. In a similar way, all the possible combinations of these x, y and z values must be summed for each concentric cube, for which there will still be a series of terms with different denominators. The concentric cube terms will converge to an answer but only slowly. The speed of the convergence can be observed using the resource in reference 2. The answer for the Madelung constant in sodium chloride is 1.74756 (six significant figures). 

Caesium chloride

Caesium chloride also adopts a cubic lattice, which lends itself to these problems, but it is slightly more difficult to work out its Madelung constant. Figure 3  shows the caesium chloride unit cell. The yellow ion represents caesium, and the green ions chloride. The ions are only drawn at half-radius size to show the structure more clearly. Red lines connect ions that are, in reality, touching. 

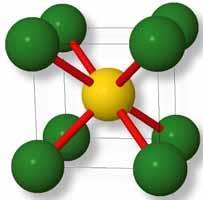
If we adopt the same system of crystal axes as we did for sodium chloride, and again take each increment of x, y and z to be half the length of the cube edge, then we can adopt a similar approach. However, in the case of caesium chloride, since the ion positions are only in cube centres and cube corners, then only certain combinations of x, y and z  will refer to ion positions. Caesium ions will only be found when x, y and z  are all even, and chloride ions only when x, y  and z are all odd. This is therefore a constraint that must be applied to any computations. We must also bear in mind that x, y and z  units of the edges of the CsCl unit cell are no longer equivalent to the internuclear distance between ions that are in contact (as was the case with the NaCl unit cell); the CsCl internuclear distance is √3 times the x,y  and z values since ions are in contact along the body diagonal of the cube. Therefore the value which this Madelung series converges to must be multiplied by √3 to give the correct value. In reference 2 the last stage of the calculation is therefore to multiply the raw Madelung constant by √3. 

The convergence problems with caesium chloride are more difficult to overcome than with sodium chloride. This is because both concentric spheres and concentric cubes of ions in the caesium chloride structure pass through positive and then negative ions in an alternating way and therefore never converge. However, by considering the positive and negative terms separately in a concentric cube calculation, the two series are seen separately to behave in a simple linear way. Taking the average of the two series of ions, we obtain the Madelung constant, which is 1.76267 (six significant figures). Since the gradients of the two series are symmetrical about the x axis² then the average of the intercepts on the y axis gives the Madelung constant. A literature search revealed that this approach has been taken before.³ 

This activity may be extended to more complicated cubic structures such as zinc blende or perovskite, where convergence problems are likely to be yet more difficult to overcome. More advanced approaches may involve engineering charge neutrality of the fragment of interest by taking fractional charges of ions in the outer layer under consideration.³ A discussion of the conditional convergence of infinite lattice sums is given in reference 4. We are currently considering the more demanding question of hexagonal lattice sums.  

Related Links

 3-D crystal structures 

Interactive 3-D crystal structures and some introductory solid state chemistry