Changing the subject

As far back as the 1970s education researchers have been highlighting and investigating students’ difficulties in applying their maths skills to other subject areas within many education frameworks.¹ It is not surprising this problem has manifested itself within STEM subjects, as an understanding of fundamental mathematical principles is a necessary building block for progression. But, despite its extensive investigation in science education research, the ‘mathematics problem’ still remains.²

Here is one of my experiences with the mathematics problem – a commonly encountered algebraic situation in high school chemistry.

How to change the subject of an equation

First, let’s look at some simple maths without any chemical context. In this example equation we want to change the subject to x, ie have x by itself on one side of the equation and everything else on the other side:

30 = 22y– 2x

There are a number of options to choose as the starting step, but recognising the convention is for the subject to be on the left, I would begin by adding 2x to both sides. I know to add 2x because it is the inverse operation of the problematic '– 2x' that I want to remove from the right hand side of the equation. This gives us:

2x + 30 = 22y

The ‘+ 30’ now needs to be dealt with. I subtract 30 from both sides, which is in line with the idea of applying the inverse operation of the troublesome term to both sides of the equation:

2x = 22y– 30

Finally, we need to liberate x from being multiplied by two by dividing both sides by two, which gives us our final answer:

x = 11y– 15

Since there are two terms on the right hand side, both are divided by two. Linguistically, this important point is reinforced as we were dividing the whole side by two, not just a portion of it – this is important for later.

This method, sometimes called the balance model, recognises algebraic manipulations must always maintain the equality of both sides of the equation.³ Whatever you do to one side you must do to the other.

The balance model in practice

I like to keep track of what I’m doing by writing the operations I do to each side of the equation at the side of the working, separated by a line for neatness. Some like to write the operation on each side, but often it ends up a little messy and difficult for another to follow the steps

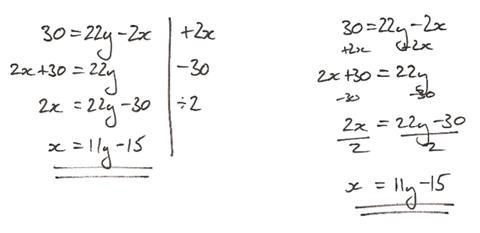
When algebra goes wrong

Let’s now look at a commonly encountered student error when trying to apply this concept in a chemistry setting. In thermodynamics, the Gibbs function, ΔG, indicates whether a reaction is feasible at a temperature, T, where the entropy and enthalpy changes for the reaction are given by ΔS and ΔH, respectively. These quantities are related to each other by:

ΔG = ΔH – TΔS

Many questions students are faced with involve the algebraic manipulation of this equation in order to change the subject, and it is when they need to find ΔS that problems arise. At some point a student should correctly identify that the term TΔS requires some action to liberate ΔS. Here is one of a number of possible incorrect algebraic paths some students may follow:

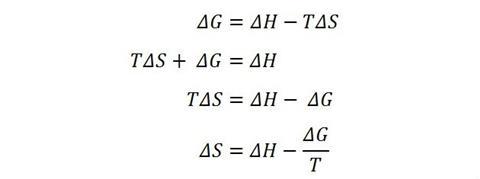
You will see the error is in the last line where the student has only divided one of the terms on the right hand side by T instead of both of them.

I have seen this problem in a number of different contexts and I think it occurs because the students are using the transition model of algebraic manipulation, more commonly called the ‘change side change sign’ rule.⁴ In this model, you identify a problematic operation and ‘move’ it to the other side of an equation. In doing so, you must change the sign so that the operation is inverted.

The problem with this method is in the notion of moving a term from one side to the other – students almost perceive the term as a physical entity as they pick it up from one side and drop it on the other. This method leaves students with little understanding of the underlying maths.

Let’s return to the final step of the incorrect rearrangement above. The student has correctly ‘picked up’ the ‘multiply by T’ and made the correct transition to ‘divide by T’ as they move it over to the right hand side. But, there is ambiguity as to where to place the ‘divide by T’, which has brought about the student’s error.

The balance model obviates this ambiguity as the operation is applied to both sides: the whole side, not just a portion of it.

Simply put, the ‘change side change sign’ model is bad. It denies students the opportunity to constantly reinforce a fundamental concept of all equations: both sides of an equation are equal.

The balance model is better and also logically extends into situations involving manipulation of trigonometric and exponential/logarithmic functions. Whereas my experience is that the ‘change side change sign’ rule results in students compartmentalising their understanding of these slightly more difficult algebraic situations, often resulting in them not recognising them as algebraic situations at all and only to be solved through another set of algorithmically applied rules.

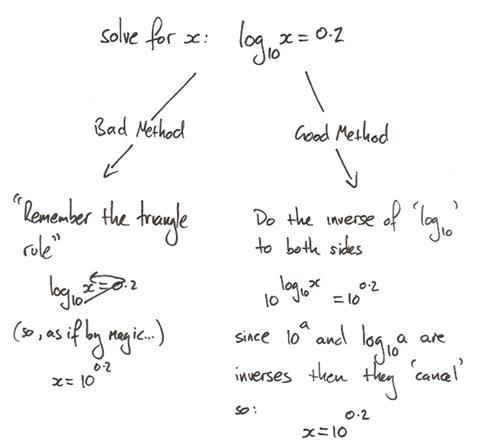
An anecdote

Communication between chemistry teachers and those teaching maths is crucial. Students’ competence with algebra will depend heavily on their maths teachers.

I was once settling in to a new school when I encountered a misalignment in the introduction of the inverse power law in the maths class and its use within certain units in chemistry. Students had not yet been taught that x^–1 is 1/x.

That particular section of the maths curriculum could have been taught much earlier, so I suggested the curriculum be reordered. The response I received was worrying: ‘That seems like a lot of work for nothing. They don’t really need to understand it, do they?’

The way forward

Unless we expect every single subject that interfaces with maths (and I’m struggling to think of any that don’t) to sort out these problems individually, then the sensible place to deal with this problem seems to be the maths classroom. However, chemistry teachers need to find ways to address these problems that we can integrate into our own practice. An awareness of the existence and origin of the ‘mathematics problem’ is a necessary first step.

Fraser Scott is a medicinal chemistry researcher, education researcher and former teacher, at the University of Strathclyde