Fractions: fear and loathing in mathematics

Despite being one of the earlier concepts met in a school career, many students have problems using fractions competently, even at undergraduate level. There is a wealth of educational research in this area.

Fractions are often conceived as being different from whole numbers, and the concepts and properties of whole numbers are regularly applied incorrectly when dealing with fractions.¹ Kristie Newton identified a persistent error in adding numerators and denominators in the addition of fractions, while Cemalettin Isik noted an ignorance of the conceptual structure of fractional division.²

A number of suggestions have been made about teaching fractions, although at a relatively early stage in students' education. These include:

• accelerating learning through the support provided by both teaching and textbooks
• students' need to gain conceptual as well as procedural knowledge
• using different representations and alternating between representations
• teaching students more than one approach to solve a task
• including activities that involve explanation and justification using words and figures

Anatomy of a fraction

Any fraction, such as 2/3, can be thought of as consisting of three parts. Symbolically

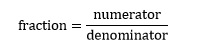
The numerator is simply the number on top, in this case 2. The denominator is 3, the number on the bottom. The third component is the horizontal line or divisor, which simply tells us that the numerical operation we are performing here is division. In this case we are dividing 2 by 3 such that

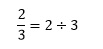
The division sign ÷ is rarely used in scientific writing – we normally express the division operation in terms of a fraction.

Manipulating fractions

The most important thing to remember when performing any operations with fractions is that we can multiply the numerator and the denominator by the same quantity and it will remain unchanged. For example

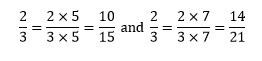
Addition and subtraction

In some ways, these are the hardest operations to perform with fractions. The critical thing to remember is that we can only add or subtract fractions that have the same denominator. So if we wish to perform the addition

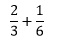
We need to recognise that

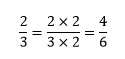
The summation then becomes

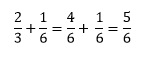
Reciprocals

The reciprocal of a fraction is simply the fraction inverted and is usually denoted by the superscript index -1. So the reciprocal of 2/3 is

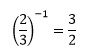
It is also possible to define the reciprocal of a non-fractional number. We can write any number in terms of a fraction with denominator 1, such as

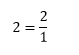
Its reciprocal is then

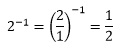
It is worth noting that if we take the reciprocal again we obtain our original number.

Multiplication and division

To multiply fractions together we simply multiply the numerators to give the final numerator, and similarly multiply the denominators to give the final denominator.

For example

To divide a fraction by another fraction, we multiply by the reciprocal of the dividing fraction. For example

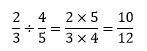
In this final example we also have the case of the resulting fraction not being the simplest possible version. Since both numerator and denominator are even, each can be divided by 2 so that

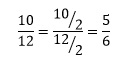
Other simplifications are generally less obvious and in chemistry it is rarely an issue to express a fraction in its simplest form. Raising a fraction to a power is a special case of multiplication. For example

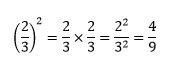
We raise the numerator to that power to give the new numerator, and the denominator to the same power to give the new denominator.

Examples in chemistry

1. Mole fractions

In a mixture of two components, 1 and 2, we can calculate the amounts of each component as n₁ and n₂. These would have units of moles. The mole fractions x₁ and x₂ of each are then defined as

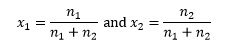
In a proprietary alcohol solution, each 100 g contains 65.0 g (1.08 mol) of isopropyl alcohol (C₃H₇OH) and 35.0 g (1.94 mol) of water.³ The mole fractions of the two components are therefore

The mole fraction has no units, and the individual mole fractions in a mixture will always add to exactly 1.

2. Spectroscopy of hydrogen-like atoms

The wavenumber, ṽ, is defined as the reciprocal of the wavelength, λ, in a spectrum:

For hydrogen-like atoms this frequency can be predicted by the Balmer-Rydberg-Ritz formula

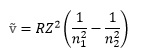
where R is the Rydberg constant (1.0974 x 10⁷ m^-1), Z is the atomic number of the element, and n₁ and n₂ are integers denoting the energy levels between which the transition takes place.

For the transition between levels 4 and 5 of hydrogen itself (Z=1) we therefore have⁴

It follows that

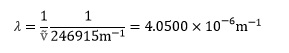
3. Arrhenius equation

This equation describes how rate constants vary with temperature, in terms of the activation energy (E_a) for a reaction. If the rate constant is k₁ at absolute temperature T₁, and k₂ at absolute temperature T₂, the equation can be written

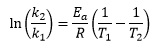
It is possible to rewrite this expression in such a way as to eliminate the reciprocal terms, if we remember that we can multiply both numerator and denominator by the same quantity. In this case we can write

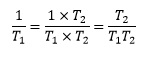
and

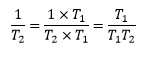
Therefore

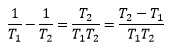
since the two terms now have the same denominator. The overall equation now becomes

For the hydrolysis of 1-chloro-1- methylcycloheptane, [(CH₂)₆CClCH₃] in ethanol, the rate constant is 3.19 x 10^-4 s^-1 at 298 K (k₁) and 2.92 x 10^-3 s^-1 at 318 K (k₂).⁵ So we calculate

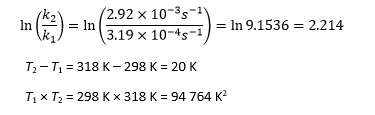
Rearranging the Arrhenius equation now gives

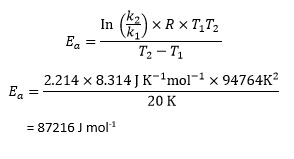
which is better expressed as 87.2 kJ mol^-1 to an appropriate number of significant figures.

Note that using this equation involves calculating T₂ – T₁ and T₁ T₂ rather than the smaller reciprocal quantities, which students may feel less comfortable dealing with.

Paul Yates is the discipline lead for the physical sciences at the Higher Education Academy.