Teaching quantitative chemistry through gases

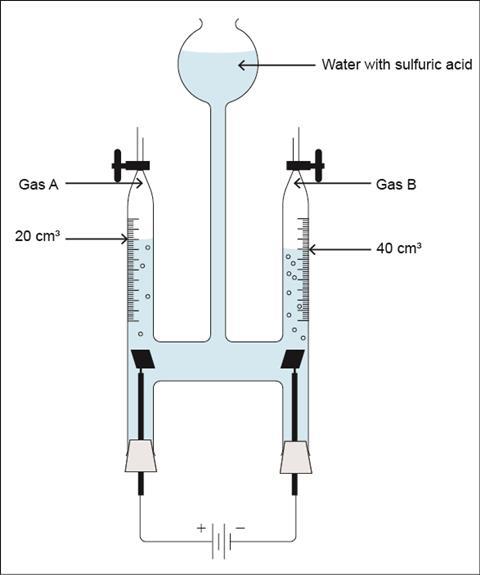
Gases provide an opportunity for students to see the link between the number of particles and a bulk property of a substance – the volume. To help students visualise this, set up a Hofmann voltameter, switch on the current, and the water will decompose into hydrogen and oxygen. Providing you have already saturated the water with dissolved oxygen beforehand (run the electrolysis for a few minutes then release the initial gas produced), hydrogen and oxygen are formed in a 2:1 volume ratio. Most students will quickly spot this ratio and relate it to the formula of water, H₂O.

There is a direct link between experimental observations and the formula of a compound. It is the ratio of two hydrogens to one oxygen in water that drives the volumes of the gases produced. The same number of hydrogen particles would occupy the same volume as any other gas. You can relate volume of gas to amount of substance (in moles) to teach your 14−16 students quantitative chemistry.

Avogadro’s law allows us to link together numbers of particles (a sub-microscopic property) with measurable volumes (a macroscopic bulk property). You can use gases to reinforce students’ understanding of ratio and how it can be applied in a chemical context. When studying the ratio of reacting volumes of gases, a balanced chemical equation gives us a wealth of information, eg the combustion of methane: CH₄(g) + 2O₂(g) → CO₂(g) + 2H₂O(g)

If we have 50 cm³ of methane, we need 100 cm³ of oxygen gas to achieve complete combustion, so twice the volume of oxygen as methane. The relationship here between the ratio of number of particles reacting and the ratio of volumes is easier to understand than when we consider the ratio of reacting masses.

What students need to know

Avogadro’s law states that the volume of a gas is proportional to the number of particles of gas. In chemistry we count particles using a unit of number called the mole. It is useful to know what volume of any gas one mole would occupy. We can then use moles to work out volume, and volume to count the particles in moles. In most pre-16 chemistry courses, we teach students that one mole of any gas occupies a volume of 24 dm³ at room temperature and pressure. For a gas:

• a decimetre (dm) is one tenth of a metre, so equal in length to 10 cm.
• a decimetre cubed (1 dm³) has the volume of a cube with sides 10 cm in length, ie 10 cm x 10 cm x 10 cm = 1000 cm³ = 1 L.

Clearing up misconceptions

Students may not consider how pressure and temperature affect the volume of a gas. They do meet these relationships in most 14−16 physics courses, but don’t always transfer this learning over to chemistry. At constant temperature, the volume of a gas is inversely proportional to the pressure – Boyle’s law. At constant pressure the volume of a gas is proportional to the absolute temperature, measured in kelvin – Charles’ law. At constant volume the pressure of a gas is proportional to the temperature – Gay-Lussac’s or the Pressure–temperature law.

Some students will not appreciate that gases have mass. You can probe this misconception with this question: when a scuba diver’s air tank is filled with pressurised air, does its weight increase or decrease?

What you need to know

Students who go on to post-16 chemistry courses are likely to learn about the ideal gas equation. This pulls together all the gas laws into a single equation.

The ideal gas equation is PV = nRT, with:

• P = pressure (Pa)
• V = volume (m³)
• n = amount of substance (mol)
• R = Gas constant = 8.31 JK⁻¹ mol⁻¹
• T = temperature (K)

In an ideal gas, the particles are treated as infinitesimally small with no forces of attraction between them. Real gases tend to behave like ideal gases, except when the pressure is very high or the temperature very low. Under these conditions the size of the gas particles and their forces of attraction mean the behaviour of real gases is no longer part of the ideal gas equation. An extreme example of this is when they condense to form liquids. While ideal gases don’t exist, they do act as a great model for real gases. Indeed, real gas properties closely follow the relationship between pressure, volume and temperature set out in the ideal gas equation over an extensive range of temperatures and pressures.

In a classic experiment, we measure the temperature and volume of a gas (at constant pressure) and then plot these data on a graph. We can extrapolate our line of best fit backward until it reaches the temperature axis (the x-axis), equivalent to a gas with zero volume. An ideal gas with zero volume contains particles that are not moving, and so are imposing no pressure on the container. This intercept on the temperature axis is hence the lowest possible temperature, termed absolute zero, and is approximately −273°C.

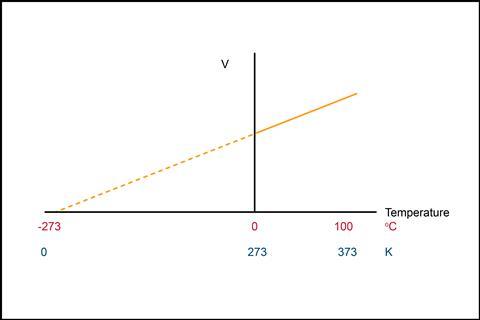
We use the kelvin temperature scale to measure absolute temperatures, starting with absolute zero as 0 K, and each 1 K increment on the scale is equivalent to 1°C. Hence: temperature (K) = temperature (°C) + 273.

It was originally thought, and is a common misconception, that at 0 K all motion would cease. Quantum mechanics tells us that we can never reach absolute zero, and even at 0 K, particles will still have a minimum energy called zero-point energy. The lowest experimental temperature so far achieved is 38 picokelvin (3.8 x 10^-11 K).

This article was updated on 11 July 2023