Mastering moles

Mole calculations at 14–16 are like Marmite. Students love them if they understand the maths they are using and can plug away at the methods successfully each time. Others, they hate them. They shrivel in fear when moles are mentioned. They refuse to engage. And they leave the ‘moles question’ blank in every practice paper.

I have even heard some teachers advise against teaching moles to so-called bottom sets as ‘they’ll never get it anyway’.

But by rethinking the way we teach moles, we can actually scaffold the concepts much better for all learners: so that higher attainers develop deeper understanding, and lower attainers tackle mole questions with confidence.

Part of the issue is the number of distinct concepts we demand students use simultaneously: Mol = mass/M_r, ratios, rearranging equations, unit conversions and determining M_r from the periodic table.

The ratio step seems to be the tipping point. Many students show an excellent standard of ‘right answerism’ with their Mol = mass/M_r calculations, but when the ratio is added it’s obvious the foundations weren’t really there. Cognitive overload ensues, and those students develop a serious allergy to moles.

For students to conceptualise mole calculations better, we need to minimise the extraneous cognitive load – by not asking them to do all these things at once, until they have really mastered the individual steps.

1 Ensure students are totally comfortable with mol = mass/M_r

Embed simple mole calculations throughout your 14–16 teaching (and even year 9) to promote mastery. Make calculating moles or M_r a normal tool for chemistry lessons long before introducing ratios.

2 Start with empirical formulas

Once students are confident using mol = mass/M_r, start determining empirical formulas. The difference between Cu₂O and CuO is much less challenging for students to conceptualise than the ratios in a balanced equation. Working through empirical formula calculations improves students’ conceptual grasp of ratios, without the demanding concept of relating that to balancing.

3 Lay out calculations properly

When you finally introduce the whole method, task students with laying out their calculations using correct mathematics and helpful notation so they can follow their own reasoning. By including units, and using notation for each line (my notation is shown in the example below), students are articulating and, consequently, reinforcing their understanding.

Hand back calculations without clear notation for students to rework. It takes too long to unpick their errors, and we need to be confident they aren’t plugging away on autopilot, but are thinking through them, linking ideas and developing schema they can draw on in future.

4 Investigate mole ratios in the lab

Relating the balanced chemical equation to the abstract ‘ratio’ is the challenge. To ensure deep learning of these tricky concepts, it is imperative we approach this ratio from as many different perspectives as possible.

In this practical, which fits easily into an hour, students complete the thermal decomposition of potassium hydrogen carbonate and use their results to identify the correct equation for the decomposition. It is squarely focused on what the balancing in a chemical equation actually means – something that many students may be able to do without sufficient understanding: a classic case of right answerism.

5 Get students to balance equations from mass data for reagents and products

This is another unusual perspective on the ratios in balanced chemical equations. In this students use the masses (or concentrations and volumes) of the reactants and products to determine the balanced chemical equation by working out the mole ratios. Students can then check their equations by balancing them normally.

But they can also use this method to determine balanced equations for reactions in which the formulas are not sufficient: cracking and incomplete combustion. Both of these kinds of reactions can be balanced in different ways if good examples are chosen; determining the mole ratio is the only way to balance them correctly.

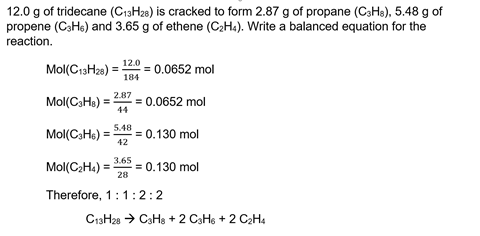
Mole ratios are a difficult concept to master. But by embracing different perspectives and dedicating time to embed foundational skills, the path to mastery can be made a little less hazardous.