Paul Yates applies this handy shorthand to chemistry calculations in mass and enthalpy

Summation is one of the earliest operations we meet in mathematics, and it may seem trivial when considering simple addition, such as:
2 + 3 = 5
But when more terms are involved, as often happens with applications in chemistry, such sums can become unwieldy. It is therefore helpful to be able to express the process more concisely.
Eighteenth century German mathematician Leonhard Euler introduced the capital Greek letter sigma, Σ, to denote a summation. The sigma is always combined with another symbol representing the quantities to be added. Therefore,
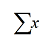
means ‘add up all the values of x’. However, without some definition of the values of x, this is pretty meaningless. We must therefore include the limits of the summation – the lower limit goes below the sigma and the upper limit above. For example,

means ‘add all the values of x from 1 to 5’ or

while
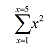
adds the squares of these numbers, so that
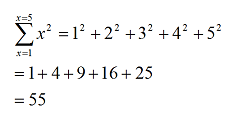
By convention, we assume x takes continuous integer values unless otherwise stated.
More commonly, the limits refer to labels on the variable. A typical example would be
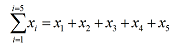
where xi represents a variable x, which can take discrete values labelled by an index variable i.
However, this complete notation is not universally applied, and it is not unusual to see several different variations. For example, when there is only a single index that varies through the sum, the index label (in this case, i) might be left out, making it slightly unclear at first glance that i is being incremented rather than x. Alternatively, the index might be specified as part of the lower limit, but implied in the upper limit. Or one or other of the limits might be omitted altogether, in which case we must rely on the context to define how far the sum should extend. While this variation in notation is potentially confusing, the meaning is usually sufficiently clear from the context.

Sigma notation is often used to describe sums of combinations of variables, linked by a common label, such as:
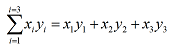
As well as providing shorthand for mathematical ideas, this notation can aid students’ understanding of mathematics.1 Steve Strand and Sean Larsen from Portland State University, US, have shown that, cognitively, the task of interpreting a given summation-notation expression differs significantly from the task of converting a longhand sum into summation notation.2
As well as providing shorthand for mathematical ideas, this notation can aid students’ understanding of mathematics. Steve Strand and Sean Larsen from Portland State University, US, have shown that (pdf), cognitively, the task of interpreting a given summation-notation expression differs significantly from the task of converting a longhand sum into summation notation.
Calculating the average mass of isotopes
The relative atomic mass, M, of an element consisting of several isotopes (labelled i) will depend on the individual mass, mi, and relative abundance, pi, of each isotope. We then have the shorthand:
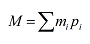
Because elements contain different numbers of isotopes, it is impossible to express a general upper limit for this sum. Although it should be self-evident we will include all the given isotopes in the list, starting with the first, we could write it with a lower limit:

Consider boron, which contains 19.9% and 80.1% . The accurate masses of the two isotopes are 10.0 and 11.0, respectively.
If we label as isotope 1 we have m1 = 10.0 and p1 = 0.199 (where this is the mole fraction, obtained by dividing the percentage by 100). Similarly, for we have m2 = 11.0 and p2 = 0.801. Since we are only considering two isotopes, the average atomic mass is given by
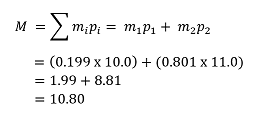
Calculating reaction enthalpy changes
Given the standard enthalpies of formation, ΔfH°, of each species in a reaction, we can calculate the standard enthalpy change for the overall reaction, ΔrH°. The enthalpy of formation of a substance at a given temperature is the change in enthalpy when one mole of the substance is formed from pure elements, with each component in its standard state (and most thermodynamically stable form) at that temperature and a pressure of 1 atm. Solutions should be present at a concentration of exactly 1 mol dm–3.
Using sigma notation, the enthalpy, ΔrH°, for a reaction, r, can be defined as:

where
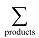
denotes the sum over all the product species, and
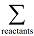
the sum over all the reactant species. ΔfHi° is the enthalpy of formation of species i. Note in this case the limit label on Σ does not relate directly to this index, but hopefully the meaning is clear from the context. The other quantity in this equation, ni, is the stoichiometric coefficient of species i in the reaction equation.
Note that the labels r and f, relating to reaction and formation, appear as subscripts to Δ, not as subscripts to H (a common error). This is because these labels apply to the change, rather than specifically to the entropy term.
To see how this works in practice, consider the reaction:
3NO2(g) + H2O(l) → 2HNO3(aq) + NO(g)
The enthalpies of formation are 33.2 kJ mol–1 for NO2(g) , –285.8 kJ mol–1 for H2O(l) , –207 kJ mol–1 for HNO3(aq) and 91.3 kJ mol–1 for NO(g). We then have, for the reactants:
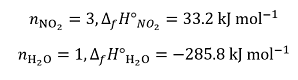
and for the products:
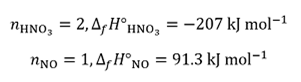
since the absence of a stoichiometric coefficient in the reaction equation implies that n = 1 for that species.
Substituting these values into the general equation
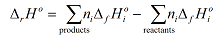
gives:
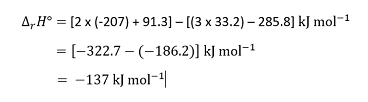
Remember subtracting a negative quantity is the same as adding the corresponding positive quantity.
An alternative way of writing the general equation for the standard enthalpy of a reaction is:
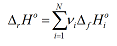
Here the sum is taken over all species in the reaction equation, on both sides. The quantity vi is the stoichiometric number, which is positive for products and negative for reactions. Therefore, in the example above:
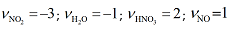
The advantage of this notation is the enthalpy of reaction can be expressed in a more rigorous mathematical way. However, splitting the sum into product and reactant terms is probably more intuitive from a chemical point of view (while also being mathematically identical).
Paul is deputy head of academic practice at Newman University
References
1. G Perlman, Mathematics Teacher, 1982, 75, 462, http://www.jstor.org/stable/27963011
2. S Strand and S Larsen, On the plus side: A cognitive model of summation notation, http://pzacad.pitzer.edu/~dbachman/RUME_XVI_Linked_Schedule/rume16_submission_82.pdf








No comments yet