Jenny Koenig explains how teachers can help students learn to rearrange equations
![Formula triangle alt 300tb[1]](https://d1ymz67w5raq8g.cloudfront.net/Pictures/480xAny/5/6/8/113568_formulatriangle_alt_300tb1.jpg)
During a university admissions interview for veterinary medicine, I asked a prospective student to explain how they would make up a solution for infusion into a dog. Part of the answer required them to work out the volume required for a given amount and concentration. The candidate started off by drawing a triangle, then hesitated, eventually giving up in despair. This was my first encounter with formula triangles.
What are they?
Formula triangles are a tool to help students use equations without needing to rearrange them. To use one, cover up the term you’re trying to find to reveal the expression required to calculate it. In the example here it’s the volume: cover up V to see the required equation is moles divided by concentration. Or if you want the number of moles, cover up the n and then, as c and V are side by side, multiply them together.
Connecting maths and science
I, and others, dislike formula triangles for a number of reasons. My experience in the admissions interview is not uncommon. While they may be a useful approach for A-level exams (these candidates all had A or A* at chemistry A-level) it doesn’t seem to help much in the long term.
They are a trick that hides the maths: students don’t apply the skills they have previously learned. This means students don’t realise how important maths is for science.1
I’m also concerned that if students can’t rearrange simple equations like the one above, they really can’t manage when equations become more complex.
Rearranging equations
Students who don’t continue to study maths after age 16 really lack confidence and fluency with algebra. For students in England and Wales, the new post-16 core maths course will be extremely important since it reinforces much of GCSE maths and focuses on applying it. Even students who study maths at A-level develop greater confidence and fluency but often find it difficult to apply their mathematical skills in other subjects.
In my experience the most successful approach to rearranging equations is the balance method. This revolves around the key idea that what you do to one side of the equation you must also do to the other (see box). Once students have mastered this technique, they can then go on to more complex equations such as rearranging the Michaelis-Menten equation to make the substrate concentration the subject.
To help students and teachers, I have several question sets in the Numbas online assessment system – click on ‘exams’ and search for ‘equations’. These questions can be downloaded and used within a website or virtual learning environment.
In my view, success in rearranging equations is more about students’ attitudes, confidence, mindset and anxiety than about any so-called natural ability. They need to understand why it is important and to realise that it is inherently simple, there are a few clear rules but no magic tricks.
How do you make V the subject of this equation?
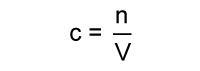
Prompt the student: What can you do to both sides of the equation to put V in the numerator?
Try multiplying both sides by V.
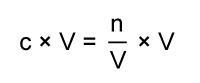
On the right hand side the Vs cancel.
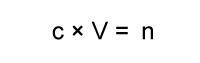
Prompt: You want V on its own, so what do you need to do to both sides of the equation?
Divide both sides by c.
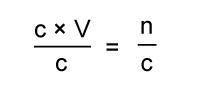
On the left hand side the cs now cancel.
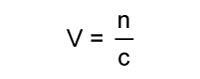
Substitute in the numbers and units, for example
n = 5x10-3 mol and c = 2 mol dm-3.

This is a long-winded approach, but when students become more confident they can skip over some of the steps.
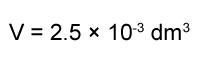
Jenny Koenig is a science education consultant and dean and director of studies in medical sciences at Lucy Cavendish College, University of Cambridge, UK
References
- J A Koenig, A survey of the mathematics landscape within bioscience undergraduate and postgraduate UK higher education. Higher Education Academy: 2011 (pdf)









2 readers' comments