On balance

Algebra is the branch of maths where letters, and other symbols, are used to represent numbers in order to construct equations and formulas. We find it many times in our chemistry curriculums: from solving PVT calculations, interpreting chemical properties graphically, through to investigating chemical kinetics.

Fundamental issues

Students find various aspects of algebra tricky. Sometimes the symbols represent physical quantities, sometimes pure numbers. This is even more challenging in chemistry because we have lots of additional uses of symbols of our own. In addition, the meaning of an algebraic expression is often not understood, ie the relationship between the various quantities.

The equals sign can also be an issue. Students often think that ‘=’ is an invitation to perform a calculation, rather than it being a symbol of equivalence.

Trouble understanding the fundamentals of algebra can mean students prefer alternative methods to solving equations when they encounter them in subjects other than maths. For example, the use of ‘magic triangles’ to solve a whole range of chemistry problems.

While ‘magic triangles’ can work in some situations, we should avoid them and instead help our students to understand the fundamental algebra. We can do this by:

• Modelling our own algebraic thinking, to make algebraic ideas explicit.
• Emphasising when symbols represent physical quantities, and when they do not.
• Asking students to describe in words what they understand by the relationships represented in symbols.

Even if you can help your students to move away from the use of magic triangles or the like and get them to approach equations more algebraically, it is important that they are doing so correctly.

Let’s change the subject

Most algebraic operations have one goal, changing the subject of the equation to a different variable. To see how your students tackle this sort of algebraic thinking, you could give them this simple diagnostic question:

Ask your students to explicitly show all working and thinking – this will quickly let you know how they approach their algebra, and if they are confident in their understanding of the underlying mathematics. Also, for this specific question, it will tease out if they are prone to using ‘magic triangles’, and if so, you can encourage them to approach the problem algebraically.

If you do persuade your students to use algebra, there is a very common approach that can lead to significant issues, and it is important that you know what it is so you can look out for it. First the correct method …

The balance model

This method recognises that algebraic manipulation of an equation must preserve the equality of both sides of the equation, ie whatever operation you do to one side you must do to the other side.

Let’s consider the following equation where we are asked to change the subject to x, ie to have x by itself on one side of the equation and everything else on the other side:

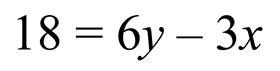
There is more than one way to approach the task, but if we recognise that the standard convention is to have the subject on the left, we will begin by adding 3x to both sides. We add 3x because it is the inverse operation of the ‘subtract 3x’ term that we want to remove from the right-hand side. Applying this operation leaves us here:

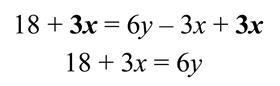
Next, we can subtract 18 from both sides of the equation. Again, we do this because we are performing the inverse operation of the ‘add 18’ term. After this operation we have:

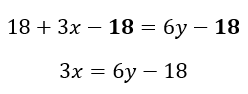
The last task is to obtain an x term, rather than a 3x term, and we do this by dividing both sides by 3. This is the inverse operation of multiplying by 3. As there are multiple terms on one side of the equation, it is important to remember that all terms are being divided by 3, not just a single term. Finally, we are left with an equation with x as the subject:

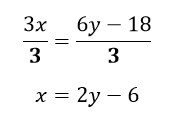
The transition model (the ‘change side change sign’ rule)

Here, we select a problematic term and ‘move’ it to the other side of the equation, and in doing so we change the sign so that the term is now the inverse operation. You may recognise this as the ‘change side change sign’ rule, and you may even have been taught it yourself. Please note that the transition model is an undesirable approach for many reasons, detailed below, and it is only explained here to help you identify if your students are using it!

Let’s do the same example as above but approach it using the transition model:

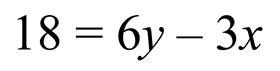
First, we will move ‘subtract 3x’ from the right-hand side to the left side of the equation, where it becomes ‘add 3x’:

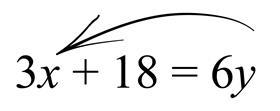
Next, we will move ‘add 18’ to the right side of the equation, which will give ‘subtract 18’. Following this, we are left with:

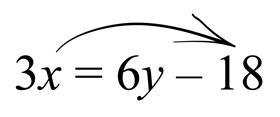
Finally, we move the ‘multiply by 3’ in front of x, to the other side, where it becomes ‘divide by 3’, and gives us the final answer as before.

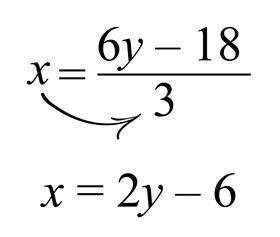
On the surface, it may seem almost identical to the balance model, but the transition model can lead to significant issues for students.

Balance model vs transition model

The most obvious problem with the transition model is that it is a ‘magic’ rule that isn’t readily understood – why does the sign change when the term moves sides? Whereas, the balance model is the fundamental framework on which the rules of algebra are built, ie for both sides of an equation to remain equal, the same operation must be performed to both sides.

A pragmatic argument could be put forward for a ‘magic’ rule as it might help a student carry out a task that they might otherwise not be able to do, ie they make the situation easier, allowing the student to get the correct answer without them necessarily understanding the underlying theory. However, in the case of the transition model, it can be the cause of some of common errors encountered in algebra.

Consider the final step in the transition model example above. When moving the ‘multiply by 3’ across to the other side, where exactly does the resultant ‘divide by 3’ go? Instead of dividing all terms by 3, many students will only divide one of the terms. This is a consequence of how they think about the process of ‘moving’ the operation from one side to another.

Similarly, consider this example where a student decides to deal with the 3 in front of the x at this stage:

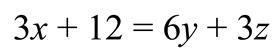
Using the transition model, a student can move the ‘multiply by 3’ to the other side, and even if they remember to divide both terms on the right by 3, the rule doesn’t allow them to correctly divide the second term, the 12, on the left hand side by 3. The transition model will always get this sort of algebraic operation wrong.

Moreover, it is not easy to extend the transition model to more challenging algebraic situations involving exponentials, logarithms or trigonometry – all of which are routinely encountered in chemistry! However, these are no trouble for the balance model.

If you spot your students using the transition model, you should encourage them to start using the balance model. To help with this, you could explicitly show them examples, like the above, where the transition model doesn’t work.

It could be that this is the method that your students have been taught. If so, perhaps a chat with your colleagues in the maths department will help. However, sometimes students simply develop this type of approach on their own.