Measuring 3D distances

While the majority of students will meet coordination geometry in their school career, only a small number will extend these principles into three dimensions. Because of this, applying coordinate geometry in three dimensions will form the focus of this article. The fundamental tool for applying coordinate geometry in chemistry is Pythagoras' theorem. You may have your own preferred way of introducing this topic, but some useful methods have been presented before.

Although we will concentrate on the underlying mathematics, it’s worth remembering that these calculations underpin all modern molecular modelling techniques. You can help your students grasp these concepts with the use of physical models, which can aid learning in both mathematics and science by helping to develop ‘three dimensional literacy’.

Locating the atom

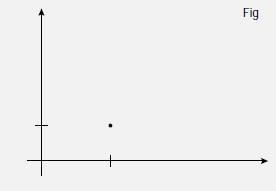
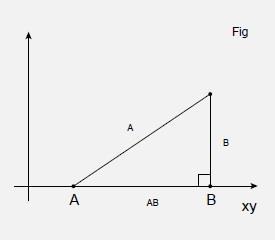
When considering molecular structure, we can define the relative positions of atoms through a system of coordinates. The most familiar coordinate system consists of two dimensions, x and y, at right angles to each other. Conventionally, x increases to the right and y increases upwards. Any point in this two dimensional system can be defined by specifying a value of x and a value of y. These values are typically grouped in brackets and separated by a comma, such as (2,1), which denotes the point A shown in Figure 1 where x = 2 and y = 1.

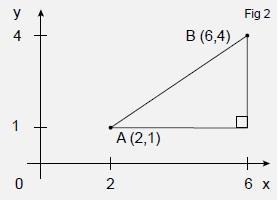
If we introduce a second point B (6,4) to this system we can measure the distance r between the points. We begin by joining the points with a straight line (Figure 2). We then draw a line parallel to the x axis and one parallel to the y axis to form a right-angled triangle as shown. From the diagram we can see that the lengths of the sides of the triangles are:

In the x direction 6 − 2 = 4

In the y direction 4 − 1 = 3

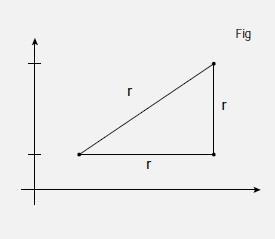
Now we can use Pythagoras' theorem to calculate the length of the longest side of the triangle, the hypotenuse. This states that if we have a right angled triangle (Figure 3) with sides r, b and c as shown, then

r² = b² + c²

In our example above, we have b = 4 and c = 3 so that

r² = 4² + 3² = 16 + 9 = 25

and so

r = 5.

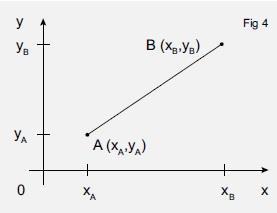
We can generalise this (Figure 4) to calculate the distance r_AB between two general points A (x_A,y_A) and B (x_B,y_B) which will be

Measuring atomic distance

This formula, in two dimensions, is useful in determining the distance between atoms in planar molecules.

Once we are dealing with physical systems we do, of course, have to consider the units. Typically, in structural chemistry problems we measure distances in nm, which is 10⁻⁹ m. In the examples that follow we will assume that all dimensions are measured in nm and will only quote the units in the final answers.

As an example, in benzene a pair of carbon atoms are found at (0.23, 0.42) and (0.30, 0.54). If we equate these to the generalised coordinates as follows:

x_A = 0.23, x_B = 0.30

y_A = 0.42, y_B = 0.54

we have

x_B− x_A = 0.30 − 0.23 = 0.07

y_B− y_A = 0.54 − 0.42 = 0.12

So, the bond length r_AB is

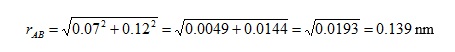
Note that since the differences, such as x_A− x_B, are squared it doesn't matter which way round we assign the atoms.

Coordinates in three dimensions

Of course, the vast majority of molecules are not planar, so we need to use a three dimensional coordinate system. While it is probably obvious that the third axis, conventionally denoted by z, needs to be at right angles to the page, it is less obvious in which direction is should be defined. By convention we choose what is called a right handed coordinate system in which the z axis increases in value as it comes out of the page as we have drawn x and y in this article.

Three dimensional problems are very difficult to represent effectively in two dimensions, and a certain amount of visualisation is needed. In Figure 5, Figure 2 has effectively been turned through 90 degrees so that we can represent the plane as a line. So, we are looking along the xy -plane, which contains the line AB. As drawn, both A and B have a z -coordinate of zero, but the same arguments will apply regardless of the z coordinate, as long as it is the same for each point so we can denote it as z_A for both A and B. This is equivalent to shifting the triangle ABC along the z axis, as in Figure 6. Now we can write the coordinates in three dimensions so that A is (x_A,y_A,z_A) and B is (x_B,y_B,z_B). A third point C has been added, which forms a right angled triangle with A and B as shown, and has coordinates (x_C,y_C,z_C). The distance between A and B is denoted as r_AB, and that between B and C as r_BC. We want to calculate the distance r_AC between A and C.

If we apply Pythagoras' Theorem to Figure 6 we have r_AC² = r_AB² + r_BC². We have already seen that

r_AB² = (x_B−x_A)² +(y_B− y_A)²

and from the coordinates of B and C we have

r_BC² = (z_C− z_B)²

Since

r_AC² = r_AB² + r_BC²

we have

r_AC² = (x_B− x_A)² +(y_B− y_A)² + (z_C− z_A)²

However, because C is directly above B it follows that x_B = x_C and y_B = y_C so

r_AC² = (x_C− x_A)² + (y_C− y_A)² + (z_C− z_A)²

With this formula we can now calculate the distance between any pair of atoms provided we know their coordinates in three dimensions. This data is frequently available from crystallographic measurements.

For example, we have a carbon atom at (0.20,0.16,0.22) and an oxygen atom at (0.24,0.18,0.35). Comparing with general coordinates gives

x_A = 0.20, x_C = 0.24 so x_C− x_A = 0.24 − 0.20 = 0.04

y_A = 0.16, y_C = 0.18 so y_C− y_A = 0.18 − 0.16 = 0.02

z_A = 0.22, z_C = 0.35 so z_C− z_A = 0.35 − 0.22 = 0.13

So

r_AC² = 0.04² + 0.02² + 0.13²

= 0.0016 + 0.0004 + 0.0169 = 0.0189

and r_AC = 0.14 nm.

Developing a feel for typical bond lengths is a useful skill in chemistry. More generally, coordinate systems can be an obstacle to understanding three dimensional structures, so this is one area where having an expectation of the correct value can be a useful aid.

Paul Yates is a consultant in academic practice at the Higher Education Academy