Alcohol and teenaged learners? A perfect mix
Ask learners to explore the six primary alcohols provided, and solve four problems based on their findings
Introduction
Teachers who have not used the problems before should read the section Using the problems before starting.
Prior knowledge
Mole concept. A detailed knowledge is unnecessary as students are encouraged to consult textbooks and data books during the exercise.
Resources
Scientific calculators; data books and textbooks should be available for reference.
Suggested approach
During trialling the following instructions were given to students and proved to be extremely effective:
- Working as a group discuss the first task and carry out the calculations. If you wish you can divide the calculations amongst yourselves and then gather the results together. Such discussion can play a vital part in working out a solution to an open-ended problem like this. Several minds working together on a problem can stimulate ideas that one on its own could not manage. A few minutes should be spent at the start discussing all the tasks with further discussion as required. Ask for help if you get stuck.
- Carry out the second task, discuss your findings and write a brief account of them.
- Repeat this process for the third and fourth tasks.
- Working as a group, prepare a short (ca 5-minute maximum) presentation to give to the rest of the class. If possible all group members should take part: any method of presentation (such as a blackboard, overhead projector, etc) can be used.
Outline the problems and describe what you did. Do not go through the detailed calculations but outline your conclusions and explain how you arrived at them. After the presentation, be prepared to accept and answer questions and to discuss what you did with the rest of the class.
Possible solutions
(i) Densities are quoted in g cm–3. The pattern emerges when molar values are considered. The molar volumes for the alcohols are given in the table below.
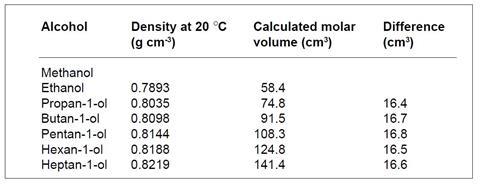
(ii) The molar volumes increase regularly because there are the same number of molecules each time, and each step down in the table represents the addition of one CH2 group to each molecule.
(iii) The volume taken up by one mole of CH2 groups is the average of the figures in the last column, 16.6 cm3. Thus the expected molar volume of methanol is 58.4 – 16.6 cm3, ie 41.8 cm3. This is the volume of one mole of molecules: to obtain the volume occupied by one molecule this figure is divided by Avogadro’s number, ie
Volume of one methanol molecule = 41.8/(6.02 x 1023)
= 6.9 x 10–23 cm3.
This volume represents the volume of the molecules including the spaces between them, so the actual volume of one molecule must be less than this.
(iv) The following are two possible solutions but students may think of others that are equally good. Both methods use atomic radii (or bond lengths).
a. Consider the ‘volume’ of a methanol molecule as the volume of a sphere with diameter equal to the distance H–C–O–H.
Radius = 0.5 { (2 x diameter of H) + diameter of C + diameter of O}
= 0.074 + 0.077 + 0.074 nm
= 0.225 nm
= 2.25 x 10–10 m
Volume of this sphere = 4/3 π r3
= 47 x 10–30 m3
= 4.7 x 10–23 cm3
Compare this with the figure of 6.9 x 10–23 cm3 calculated from the molar volume in (iii) above.
b. Consider the ‘volume’ of a methanol molecule as made up of two parts, CH3 and OH. The total volume is taken as the volume of two spheres touching one another – one (the CH3 group) swept out by the C–H bonds, the other (the OH group) the volume of an oxygen atom.
Radius of CH sphere = radius of C + (2 x radius of H)
= 0.077 + 0.074 nm
= 0.151 nm
= 1.51 x 10–10 m
Volume of sphere = 4/3 π r3
= 14.4 x 10–30 m3
= 1.4 x 10–23 cm3
Radius of OH sphere = radius of O + 2 x radius of H
= 0.074 + 0.074 nm
= 0.148 nm
Volume of sphere = 1.4 x 10–23 cm3
Total volume = 1.4 x 10–23 + 1.4 x 10–23 cm3
= 2.8 x 10–23 cm3
ie Volume of one methanol molecule is 6.9 x 10–23 cm3 from molar volumes ((iii) above); 4.7 x 10–23 cm3 from atomic radii assuming a spherical molecule ((iv)a. above); 2.8 x 10–23 cm3 from atomic radii assuming two spheres touching ((iv)b. above).
The first estimate is larger than the other two because it includes the space between the molecules.
Dulong and Petit’ s Law
It is interesting to compare the pattern in these figures with those in ‘Find the pattern – metals’ (Dulong and Petit’s Law). In the latter case, the heat required to raise the temperature of a metal is proportional to the number of atoms and does not depend on what these species are, ie the molar heat capacity for the metals is roughly constant (26 J mol–1 K–1). In this case the molar volumes increase regularly and it is the differences between the values for homologues (16.6 cm3) that are roughly constant.
Possible extension
If students have tackled both ‘Find the pattern’ problems they could be asked to explain the difference and to predict what pattern molar enthalpies of combustion of these alcohols are likely to follow.
Downloads
Find the pattern - alcohols - creative problem-solving
PDF, Size 0.26 mb
Additional information
This resource is part of our Creative problem-solving in chemistry collection.

















No comments yet