Working with units and prefixes

A measurement without a unit is meaningless. If you ask me how tall I am and I say ‘168’, it doesn’t help much until I add the units: centimetres. In this article, I will consider how to help students consistently use units and prefixes correctly and easily convert between them.

Progression

At primary school, the English national curriculum includes making measurements using mm, cm, m, ml, l, g, kg and converting between the units with different prefixes. It also includes calculating area in cm² or m² and volume in cm³ and m³. However, it’s not always clear how secure this knowledge is, how much experience students have had of making measurements using a variety of units, or how well they are able to make good estimations. Therefore, at the beginning of secondary science it is a good idea to review and consolidate both estimating measurements and making careful measurements. It’s also useful in early secondary to introduce decimetres explicitly, as students are unlikely to have much experience of making measurements in dm and dm³ replaces the use of litres as a measure of capacity.

Developing multiplicative reasoning

Sometimes students struggle to understand that prefixes (eg milli, centi, deci, kilo) are separate entities from the units (metre, gram, litre etc) and that the prefix acts as a multiplier of the unit – that centi means a hundredth and a cm is a hundredth of a metre. Confusion sometimes arises because m stands for both milli and metre. At the beginning of secondary school students may be familiar with mm in the context of length but might not have seen mg in the context of mass.

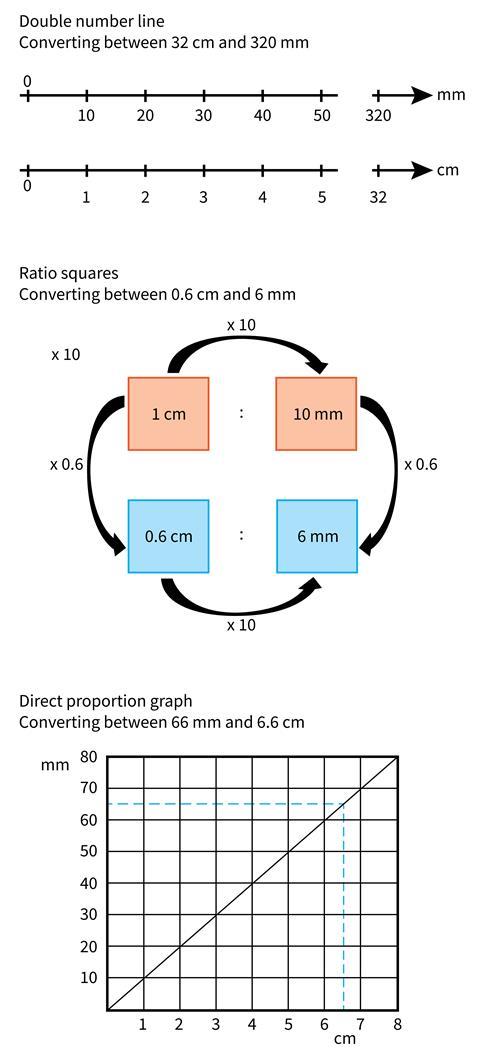
Multiplicative reasoning is helpful when converting between units, and visual representations such as a double number line, a graphical approach or ratio squares can be good ways of developing this reasoning and reinforcing mathematical concepts in science lessons. Figure 1 shows these three visual supports for converting between units. This is an area where departments could collaborate to ensure that maths and science lessons support each other.

Another way of demonstrating this is shown in Figure 2. In lessons it might be helpful to provide the whole diagram to begin with, then cover up either the prefixes and units, the multipliers, or indeed the directions of the arrows and ask students to identify what has been covered up. Use this diagram alongside the questions in the download, Practice with units and prefixes.

Linking units with formulas

When using formulas, it is important to introduce the units at the same time and to show how the units relate to the formula. For example, concentration can be expressed as mass per volume. Since mass is measured in grams and volume is measured in dm³ (or cm³), the concentration is given in g.dm^-3 (or g.cm^-3).

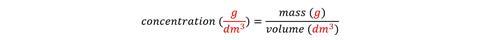
Indeed, the units for concentration are a giveaway if you can’t remember the formula.

For many students, the idea that a negative power indicates a reciprocal is something of a mystery. Therefore, it is worth pointing out that g.dm^-3 is the same as g/dm³ (and g.cm^-3 is the same as g/cm³) and they are both spoken as ‘grams per decimetre cubed’ (or ‘grams per centimetre cubed’).

When modelling solutions to problems, make sure you show units throughout the workings out. This will help to reinforce the importance of including units with numerical answers and ensuring that they cancel out appropriately to end up with the unit you would expect.

mass = concentration x volume = 5 g.dm^-3 x 30 dm³ = 150 g

When converting between moles and mass, it’s helpful to use the molar mass, which has the units of g.mol^-1, rather than the relative molecular mass which has no units. Indeed the formula relating mass and moles can be written:

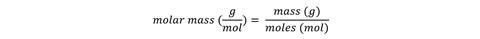
Unfortunately, in maths and some science GCSE exam papers, the unit is given on the answer line – this is unfortunate because students feel they don’t need to worry about it. It would help to design assessments so that the student is expected to report both number and unit and the mark scheme gives credit to both.