Defining a ‘weak’ acid

Look up any monoprotic (monobasic) weak acid in a data book. Starting from its K_a (or pK_a) value, calculate or find as much information as you need to show what is meant by ‘weak’ in weak acid.

Introduction

This problem contains little information. Students will have to recall information learned earlier in their course about solution chemistry, pH and weak acids or find the information in textbooks, and then apply this knowledge to the problem in a creative way.

Teachers who have not used the problems before should read the section Using the problems before starting.

Prior knowledge

Solution chemistry ie weak acids and strong acids, Ka (or pKa) and pH. A detailed knowledge is unnecessary as students are encouraged to consult textbooks and data books during the exercise.

Equipment

Scientific calculators, data books to look up strengths of weak acids and physical chemistry textbooks should be available for reference.

Possible solutions

Students should refer to data books and select a suitable acid. Possibilities include:

Acid	Ka	pKa1
Aminoethanoic	1.4 x 10-10	9.87
Boric2	7.2 x 10-10	9.14
Ethanoic	1.4 x 10-5	4.76
Hydrocyanic	4.9 x 10-10	9.31
Nitrous	5.4 x 10-4	3.27
Phenol	1.0 x 10-10	10.00

This example concerns an aqueous solution of HCN³

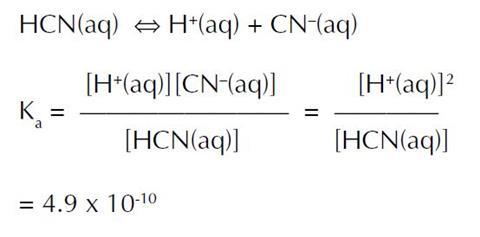
Students will have to decide on the concentration of the acid solution, 0.10 mol dm^–3 will be used in the following calculations:

[H⁺(aq)]² = 4.9 x 10^–10 x 0.10 (assuming little HCN dissociates)

[H⁺(aq)] = 7.0 x 10^–6 mol dm^–3 (pH = 5.2)

(This ignores the contribution of the ionisation of water to the concentration of H⁺(aq) – a reasonable assumption even for phenol)

To show what this means, students could:

1. compare this figure with say water and a strong acid, or
2. manipulate the figures for the acid itself.

a. comparing the weak acid with water and a strong acid

In water, [H⁺(aq)] = 1.0 x 10^–7 mol dm^–3

0.1 mol dm^–3 HCN, [H⁺(aq)] = 7.0 x 10^–6 mol dm^–3

0.1 mol dm^–3 HCl, [H⁺(aq)] = 1.0 x 10^–1 mol dm^–3

The ratio of [H+(aq)] in the three liquids is

1.0 x 10^–7 : 7.0 x 10^–6 : 1.0 x 10^–1

or 1 : 70 : 1 000 000

This shows that the weak acid is closer to water than to a strong acid in terms of H⁺(aq) ion concentration. For every H⁺(aq) in the HCN, there are about 14 000 H⁺(aq) in the HCl. Students who use this approach should attempt to put the numbers into context, eg:

• 14 000 is the approximate number of students at a university such as Glasgow; and
• the contents of 14 000 one litre bottles of lemonade would occupy a cube with side 2.5 m.

b. manipulating the figures for the weak acid

The cyanide ion concentration is the same as [H⁺(aq)] ie 7.0 x 10^–6 mol dm^–3, and the concentration of unionised HCN is 0.10 – 7.0 x 10^–6 mol dm^–3, effectively 0.10 mol dm^–3. Students have been asked to consider the number of ions and molecules in a solution, so they will use Avogadro’s number; they could also calculate the figures for a smaller volume, eg or 1 cm³ or 1 drop.

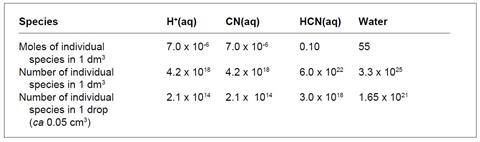
Compare these figures with:

• the UN estimate for the 1990 world population of 5.25 x 109;
• the Earth–Sun distance of 1.5 x 1011 m; and
• the distance to the nearest star (Proxima Centauri) is 1.5 x 1017 m.

See note 5 for calculation of α, the degree of dissociation of the acid.

To get meaningful numbers, students could calculate ratios from the table, such as:

• for every H⁺(aq) ion there are 3.3 x 1025/4.2 x 1018 (about 8 million) molecules of water;
• for every H⁺(aq) ion there are 6 x 1022/4.2 x 1018 (about 14 000) molecules of HCN; and
• for every HCN molecule there are 3.3 x 1025/6.0 x 1022 (about 555) molecules of water.

These ratios are more meaningful than the raw numbers and could form the basis of a group’s presentation. The first figure (8 million) is comparable with the population of:

• Greater London (6.4 million);
• Scotland (5 million); and
• Eire (3.5 million).