Find the pattern - metals

Look for patterns in the specific heat capacities of metals, and then propose an explanation for the pattern.

Introduction

Teachers who have not used the problems before should read the section Using the problems before starting.

Prior knowledge

Mole concept and specific heat capacity. A detailed knowledge is unnecessary as students are encouraged to consult textbooks and data books during the exercise.

Resources

Specific calculators; data books and textbooks should be available for reference.

Suggested approach

During trialling the following instructions were given to students and proved to be extremely effective:

1. Working as a group discuss the first task. Look for patterns and suggest an explanation. Ask for help if you get stuck. Such discussion can play a vital part in working out a solution to an open-ended problem like this. Several minds working on a problem can stimulate ideas that one on its own could not manage. About 10 minutes should be spent on this initially, with further discussion as required.
2. Write a brief account of your findings.
3. Repeat this process for the second task and the third task.
4. Working as a group, prepare a short (ca 5-minute maximum) presentation to give to the rest of the class. If possible all group members should take part: any method of presentation (such as a blackboard, overhead projector, etc) can be used.

Outline the problem and describe what you did. Do not go through the detailed calculations but outline your conclusions and explain how you arrived at them. After the presentation, be prepared to accept and answer questions and to discuss what you did with the rest of the class.

Background information

Dulong and Petit’s Law 1

This generalisation states that ‘for all solid elements the product of the atomic weight and the specific heat is a constant, approximately 6.3’. This figure is cal mol^–1 K^–1; the corresponding figure using joules is as calculated above – approximately 26 J mol^–1 K^–1. At that time (1819) it was easy to determine the ‘equivalent weight’ of an element experimentally but difficult to obtain the atomic weight from it. Dulong and Petit’s Law allowed this conversion for many solid elements. Consider, for example, copper which forms two series of compounds where the equivalent of copper is 31.75 and 63.5 respectively. From this it is evident that the atomic mass is some multiple of 31.75 ie 63.5 or 95.25 or 127 etc. The specific heat capacity of copper is 0.09 cal mol^–1 K^–1; thus the atomic mass is approximately 6.3/0.09 or 70, and the accurate atomic mass is 63.5.

Problems arose because of the variation of specific heat capacity with temperature, and elements with high melting point (eg carbon and beryllium) were exceptions to the law when the specific heat capacity was measured at normal temperatures. It has since been shown that these elements ‘fit’ the law when their specific heat capacities are determined at high temperature.

Possible solutions

(i) The key fact here is that the figures are quoted per kilogram rather than per mole. The pattern emerges when molar values are considered.

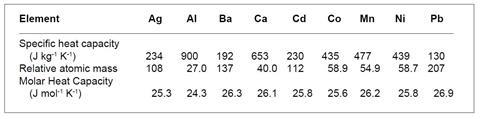
The mean value of the molar heat capacity is 25.8 J mol^–1 K^–1.

From these figures it is clear that the heat required to raise the temperature of a metal depends on the number of atoms and not on what the atoms are. This is in fact Dulong and Petit’s Law of 1819.

(ii) The specific heat capacity of the unknown metal is 385 J kg^–1 K^–1

The calculated atomic mass is 25.8 x 1000/385 = 67.0

The element could be zinc (65.4), gallium (69.7) or perhaps copper (63.5).

(iii) To answer this question:

Chemical tests could be used; and a data book can be consulted for the specific heat capacity. The figures found were: zinc = 385; gallium = 381; copper = 385 J kg^–1 K^–1.