Try this experiment with your students to measure the hardness of different water samples and investigate the effect of boiling hard water
This is a student practical, where a lot of the preparation work has been done beforehand. It could be varied so that the students watched, or carried out themselves, the preparation of the solutions. This would require using real (or simulated) sea water, rather than mixing temporarily and permanently hard water. The temporarily hard water will also really need to be boiled and cooled (as opposed to distilled water being substituted).
For younger, or less practically experienced students, consider providing the burettes already clamped and full of soap solution.
Students should bring their conical flasks to the stock bottles of solutions A to E and use a dedicated measuring cylinder for each solution to obtain 10 cm3. With larger groups, consider telling different groups to start with a different letter.
The work as described will take about 45 minutes.
Equipment
Apparatus
- Eye protection
- Measuring cylinders (10 cm3), x5 (one for each of the solutions A to E)
- Conical flask (100 cm3)
- Bung, to fit the conical flask
- Burette and burette stand
- Small funnel
Chemicals
- Soap solution in IDA (industrial denatured alcohol), (HIGHLY FLAMABLE, HARMFUL), 75 cm3 per group (see note 3)
- A supply of distilled or deionised water for rinsing flasks between experiments
- Solutions as follows, about 20 cm3 per group:
- Solution A: deionised water, labelled as ‘Rain water’
- Solution B: a 50:50 mixture of temporarily and permanently hard water, labelled as ‘Sea water’
- Solution C: temporarily hard water, labelled as ‘Temporarily hard water’
- Solution D: deionised water, labelled as ‘Boiled temporarily hard water’
- Solution E: permanently hard water, diluted 50:50 with deionised water and labelled as ‘Boiled sea water’
Health, safety and technical notes
- Read our standard health and safety guidance.
- Wear eye protection throughout.
- Soap solution in ‘ethanol’ (industrial denatured alcohol, IDA – see CLEAPSS Hazcard HC040A, HIGHLY FLAMMABLE, HARMFUL) can be purchased or made up. Genuine liquid soap or soap flakes, from which the liquid can be made, are increasingly difficult to obtain. Wanklyn’s and Clarke’s soap solutions should still be available from chemical suppliers. Lux soap flakes are ideal for making liquid soap if you can source them. Granny’s Original and other non-branded soap flakes work fine but need to be used in solution as soon as they are made. They do not form a stable emulsion and precipitate out overnight. Note that most liquid hand washes are based on the same detergents as washing-up liquids and do not contain soap. To obtain soap solution from soap flakes, dissolve soap flakes (or shavings from a bar of soap) in ethanol (use IDA). See CLEAPSS Recipe Book RB000. Do not dissolve in water.
- Dilute about 150 cm3 of limewater (IRRITANT, see note 5) with an equal volume of distilled water. Pass in carbon dioxide (see Generating, collecting and testing gases), taking care that the gas carries over no acid spray, whereupon calcium carbonate is soon precipitated. Continue the passage of gas until all the precipitate dissolves, giving a solution of calcium hydrogen carbonate. This is temporarily hard water.
- Limewater (calcium hydroxide solution) (IRRITANT) – see CLEAPSS Hazcard HC018 and CLEAPSS Recipe Book RB020.
- Stir a spatula or two of hydrated calcium sulfate – see CLEAPSS Hazcard HC019B – into some deionised water. Swirl to mix, allow to stand, then decant off the clear solution. This is permanently hard water.
Procedure
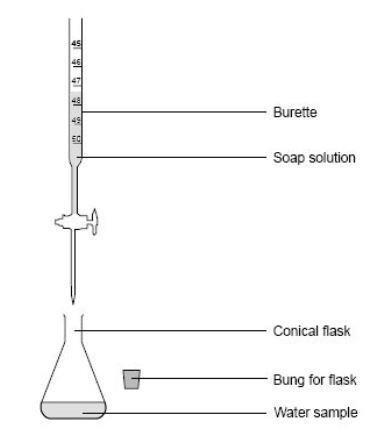
- Collect about 75 cm3 of soap solution in a small beaker.
- Set up a burette and, using the small funnel, fill it with soap solution.
- Use a measuring cylinder to measure out 10 cm3 of one of the samples of water from the list below into a conical flask:
- Rain water (solution A)
- Sea water (solution B)
- Temporarily hard water (solution C)
- Boiled temporarily hard water (solution D)
- Boiled sea water (solution E)
- Read the burette. Add 1 cm3 of soap solution to the water in the conical flask. Stopper the flask and shake it. If a lather appears that lasts for 30 seconds, stop and read the burette.
- If no lather forms, add another 1 cm3 of soap solution. Shake the flask. Repeat the process until a lather forms that lasts for 30 seconds. Read the burette.
- Rinse out the flask with distilled water. Repeat the experiment with 10 cm3 of another water sample, until you have tested them all. Make a note of the volumes of soap solution that were needed in each case to produce a lather.
- From your experiments, decide:
- Which water samples are ‘soft’ and why
- Whether sea water contains permanent hardness, temporary hardness or a mixture of both.
Teaching notes
Sample A will require very little soap solution. This shows that rain water is soft. It has effectively been distilled (and like distilled water, it will contain dissolved carbon dioxide but no salts).
Sample D will also require very little soap. This shows that temporarily hard water can be softened by boiling (see theory below).
The other samples will require more soap but E will require less than B, showing that sea water contains both temporary and permanent hardness.
The volumes of soap solution needed give a measure of the relative hardness of the various samples. With more able groups, it might be worth considering that rainwater is completely soft, so that the volume of soap required here is just the amount required to get a lather, not to overcome hardness. This volume should be subtracted from the other volumes before the relative hardnesses are compared.
Hard water contains dissolved calcium (or magnesium) salts that react with soap solution to form an insoluble scum that should be seen as a white cloudiness in the tubes:
calcium salt(aq) + sodium stearate (soap)(aq) → calcium stearate (scum)(s) + sodium salt(aq)
Only when all the calcium ions have been precipitated out as scum will the water lather. Thus the volume of soap solution measures the amount of hardness.
Temporarily hard water is defined as that which can be softened by boiling. The reactions by which it is made here are:
Ca(OH)2(aq) + CO2(g) → CaCO3(s) + H2O(l)
(Calcium carbonate is the ‘milkiness’ that forms when lime water is reacted with carbon dioxide.)
CaCO3(s) + CO2(g) + H2O(l) → Ca(HCO3)2(aq) (calcium hydrogen carbonate)
This reaction also occurs when rain water (containing dissolved carbon dioxide) flows over limestone rocks. On boiling, the reaction is reversed, softening the water:
Ca(HCO3)2(aq) → CaCO3(s) + CO2(g) + H2O(l)
Permanently hard water contains calcium or magnesium salts other than the hydrogen carbonates. These are unaffected by boiling.
Additional information
This is a resource from the Practical Chemistry project, developed by the Nuffield Foundation and the Royal Society of Chemistry.
Practical Chemistry activities accompany Practical Physics and Practical Biology.
© Nuffield Foundation and the Royal Society of Chemistry
















No comments yet