Have a go at a past Chemistry Olympiad question using this worked example, investigating the properties of ingredients in sherbet lemons
In this question from the 2006 UK Chemistry Olympiad round one paper, students apply their knowledge and understanding of a number of the ingredients in sherbet lemons to write a combustion equation for sugar, calculate energy released and investigate the structures of tartaric acid and citric acid. The accompanying video walkthrough is designed to help students if they get stuck or want to check their working.
The question is of low difficulty, and covers the following chemistry topics:
- Balancing combustion equations
- Thermodynamic calculations
- Mole calculations
- The structures of tartaric acid and citric acid
What’s on this page?
- How to use this resource
- Question
- Answers
- Walkthrough (including video and transcript)
How to use this resource
Find out more about how to use Chemistry Olympiad worked answers.
Note
This question first appeared as question 1 in the 2006 UK Chemistry Olympiad round one paper. For marking, including notes on allowances, see question 1 in the 2006 examiners’ mark scheme.
Question
Sherbet lemons are sweets which consist of a flavoured sugar shell filled with sherbet. The sherbet contains sodium hydrogencarbonate and tartaric acid (2,3-dihydroxybutanedioic acid).
Part a
Assuming all the sugar present is sucrose, C12H22O11, write an equation for the complete combustion of the sugar.
Part b
The standard enthalpy change of combustion of sucrose is –5644 kJ mol–1. Calculate the energy released when one sweet containing 6.70 g of sucrose is completely burnt.
Part c
A man needs to consume about 2500 dietary calories per day. Given that 1 kJ ≡ 0.239 dietary calories, how many sweets must a man consume in order to meet his daily calorific requirement?
Part d
Sherbet produces a slight fizzing sensation in the mouth when the tartaric acid reacts with the sodium hydrogencarbonate to make carbon dioxide. In a laboratory experiment, one sherbet lemon sweet produced 6.00 cm3 of carbon dioxide.
Calculate the minimum masses of tartaric acid and sodium hydrogencarbonate necessary to produce this volume of carbon dioxide. (Assume 1 mol of any gas occupies 24.0 dm3 at r.t.p.)
Part e
A carbon atom bonded to four different groups is called a chiral centre or an asymmetric carbon atom. A molecule which contains just one chiral centre exists as two stereoisomers (isomers containing the same groups attached to the same atoms). These stereoisomers are non-superimposable mirror images of each other called enantiomers. If a molecule contains more than one chiral centre, the number of stereoisomers increases and some of the stereoisomers may be superimposable on their mirror images.
By making the appropriate substitutions for a, b, c, and d in the structure shown below, draw all the different stereoisomers of tartaric acid, indicating clearly which (if any) are enantiomers.
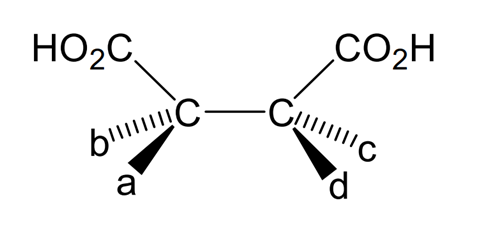
Part f
Citric acid is used to flavour sherbet lemons. Its formula may be written HOOCCH2.C(OH)(COOH).CH2COOH. How many asymmetric carbon atoms does this molecule contain?
Answers
Part a
C12H22O11 + 12O2 → 12CO2 + 11H2O
Part b
110 kJ or 111 kJ (rounded to 3 sig fig)
Part c
95 sweets
Part d
Mass of sodium hydrogencarbonate = 0.0210g
Mass of tartaric acid = 0.0188g
Part e

Part f
None
Walkthrough
Transcript
Download this
Introduction
This question is about sherbet lemons.
In the introduction, you are introduced to sherbet lemons as sweets which consist of a flavoured sugar shell filled with sherbet. The sherbet contains a mixture of sodium hydrogencarbonate and tartaric acid.
Part a
In part (a) of the question you are asked to write an equation for the complete combustion of the sugar in the sherbet lemon, which is assumed to be sucrose, C12H22O11. For combustion of an organic compound such as sucrose, we know that oxygen is required and that the products of the combustion are carbon dioxide and water. Hence we can write the equation, sucrose plus oxygen forms carbon dioxide and water.
All that remains now is to balance the equation by ensuring that there are the same number of each type of atom on either side of the equation. Running through each element in turn, there are 12 carbon atoms on the left and so 12 molecules of carbon dioxide, each containing one carbon atom must be formed; one molecule of sucrose contains 22 hydrogen atoms and so 11 molecules of water each containing 2 hydrogen atoms must be formed, and then finally balancing the oxygen atoms, the products from the reaction contain (12 × 2) + 11 = 35 atoms of oxygen. Sucrose itself contains 11 atoms, which means that 24 atoms of oxygen must be added from the oxygen gas, and so the reaction must involve 12 molecules of oxygen.
Part b
Part (b) of the question moves on to look at the energy released in this reaction. You are asked to calculate the energy released when one sweet is completely burnt, given that one sweet contains 6.70 g of sucrose and that the standard enthalpy change of combustion of sucrose is -5644 kJ mol-1. The standard enthalpy change of combustion of sucrose tells us that when one mole of sucrose undergoes complete combustion under standard conditions, 5,644 kJ of energy are released. Therefore to calculate how much energy is released by 6.70 g it is necessary to find the number of moles in this mass of sucrose. This can be calculated by dividing the mass of sucrose, 6.70 g by its molar mass. The molar mass of a substance is equal to the relative molecular mass of that substance given in grams. Therefore, using the molecular formula given for sucrose in part(a) of C12H22O11, we can calculate the molar mass of sucrose to be 342.296 g mol-1. Therefore substituting this value into our equation at the start of the question, we can calculate the number of moles in 6.70 g of sucrose to be 0.0196 moles. Finally, then if we know that one mole of sucrose releases 5644 kJ of energy, then 0.0196 moles will release 0.0196 moles × 5644 kJ mol-1 of energy = 110.47 kJ or 110 kJ to 3 significant figures, which is to the same degree of accuracy as the 6.70 g of sucrose that the calculation is based on.
Part c
In part (c) of the question, you are then asked to use this value to calculate the number of sweets a man must consume in order to meet his daily calorific requirement, given that a man needs to consume 2,500 dietary calories a day and that 1 kJ = 0.239 dietary calories. The first step then is to convert the energy released by one sweet of 110.47 kJ into dietary calories by multiplying 110 kJ by 0.239 dietary calories per kJ and if we do this sum we calculate that each sweet contains 26.40 dietary calories. Therefore, if a man needs to consume 2,500 dietary calories a day, then the number of sweets he must consume is 2,500 calories per day ÷ 26.40 calories per sweet which gives us a final answer of 94.68 sweets per day or 95 sweets to the nearest whole sweet.
Part d
Part (d) the question moves on to look at the chemistry of the reaction that produces a slight fizzing sensation when you place a sherbet lemon in your mouth. The fizzing sensation is caused by the reaction of the tartaric acid with the sodium hydrogencarbonate which releases carbon dioxide. A laboratory experiment has shown that a single sherbet lemon produces 6.00 cm3 of carbon dioxide. The question asks you to calculate the minimum masses of tartaric acid and sodium hydrogencarbonate necessary to produce this volume of gas.
The first challenge with this question is to write out a balanced equation for the reaction between tartaric acid and sodium hydrogencarbonate. The formal name for tartaric acid is given in the introduction to the question as 2,3-dihydroxybutanedioic acid. Therefore we can draw out a structural formula for the molecule. The longest carbon backbone is 4 atoms (butane), it’s a dioic acid and so there must be a carboxylic acid group on each end, and the prefix of 2,3-dihydroxy tells us that there must be a hydroxyl group on carbon atoms 2 and 3. When sodium hydrogencarbonate reacts with an acid, let’s call the acid, HA, the products from the reaction are a salt formed from the Na+ cation and A– anion, carbon dioxide and water. Since the tartaric acid contains two acidic hydrogen atoms, it’s a diprotic acid and so we must adapt our equation to show this by changing the acid to H2A and the salt to Na2A. Since one mole of sodium hydrogencarbonate reacts with one mole of protons, and each mole of the diacid contains two moles of protons, then two moles of sodium hydrogencarbonate must react, producing two moles of water and two moles of carbon dioxide.
We can now use this equation to write out a full equation for the reaction between tartaric acid and sodium hydrogencarbonate of one mole of tartaric acid reacts with 2 moles of sodium hydrogencarbonate to produce one mole of salt, two moles of carbon dioxide and two moles of water. We can now use this balanced equation for the reaction to calculate the minimum masses of tartaric acid and sodium hydrogencarbonate required to produce 6.00 cm3 of carbon dioxide. First we need to convert the volume of 6.00 cm3 into a number of moles. Since one mole of any gas has a volume of 24.0 dm3 or 24,000 cm3 at room temperature and pressure, we can calculate that the number of moles in 6.00 cm3 of gas under these conditions is 2.5 × 10–4 mol.
Looking now at the stoichiometry of the reaction, we can see that one mole of tartaric acid reacts with two moles of sodium hydrogencarbonate to produce two moles of carbon dioxide. Therefore we know that the number of moles of tartaric acid which must react is 2.5 × 10–4 ÷ 2 = 1.25 × 10–4 moles and that the number of moles of sodium hydrogencarbonate required is 2.5 × 10–4.
Finally then, we need to convert each of these number of moles into a mass which can be achieved by multiplying the number of moles by the molar mass of each substance. Using the relative atomic masses for C, H, O and Na given in the periodic table at the start of the question paper, we can calculate the molar mass of tartaric acid to be 150.088 g mol–1 and the molar mass of NaHCO3 to be 84.008 g mol–1. Therefore we can calculate that the mass of tartaric acid needed is 1.25 × 10–4 mol × 150.088 g mol–1 = 0.0188 g and the mass of sodium hydrogencarbonate needed is 2.5 × 10–4 × 84.008 g mol–1 = 0.0210 g (both answers given to 3 significant figures to match the accuracy for the volume of carbon dioxide measured given in the question).
Part e
The final part of the question looks at the structure of the tartaric acid in more detail. In the introduction, you are told that a carbon atom bonded to four different groups is called a chiral or an asymmetric carbon atom. A molecule which contains just one chiral centre exists as two stereoisomers. These stereoisomers are non-superimposable mirror images of each other and are called enantiomers. If a molecule contains more than one chiral centre, the number of stereoisomers increases and some of the stereoisomers may be superimposable on their mirror images.
Part (e) of the question asks you to look at the structure of tartaric acid and by making substitutions for a, b, c, and d to draw all the different stereoisomers of tartaric acid. From the formal name for tartaric acid given in the introduction, we know that the molecule contains a hydroxyl group at carbon atoms 2 and 3. Therefore we can draw out for different structures, the first two with the same stereochemistry at carbon 2 but different stereochemistry at carbon 3, and vice versa for the latter two structures. If we look at these structures in more detail however, we can see that structures 1 and 4 are in fact identical – by rotating structure 1 by 180° you would obtain structure 4. This is because the molecule contains a plane of symmetry. Therefore there are only 3 possible structures. If we draw them out again, we can see that compounds 2 and 3 are mirror images of each other, and so we can label them as a pair of enantiomers. Compound 1 or 4 is achiral or does not exist as enantiomers despite the fact that it contains two chiral centres. Molecules such as this which are achiral as a result of a plane of symmetry despite containing chiral centres fall into a special group and are called meso compounds. Therefore we can say that tartaric acid exists in three stereoisomeric configurations, two enantiomers and one meso compound.
Part f
Part (f) of the question introduces a final molecule, citric acid which is used to flavour sherbet lemons. The question gives you the formula for citric acid and asks you how many asymmetric carbon atoms it contains. If we draw out the structure of the citric acid we can look at each carbon atom in turn. Remember that for a carbon atom to be asymmetric or chiral it must be bonded to four different groups. Therefore, looking at each of the carbon atoms in turn, the two carbon atoms at either end of the molecule are not chiral because they are each bonded to two hydrogen atoms. Similarly the carbon atom in the centre is not chiral because it is bonded to two matching CH2COOH groups on either side. Therefore we can say that there are no asymmetric carbon atoms in citric acid.
Downloads
Thermodynamic calculations and sherbet lemons - video transcript
Editable handout | Word, Size 0.98 mbThermodynamic calculations and sherbet lemons - video transcript
Handout | PDF, Size 0.62 mb
Chemistry Olympiad worked answers
- 1
- 2
 Currently reading
Currently readingThermodynamic calculations and sherbet lemons
- 3
- 4
- 5
- 6
- 7
- 8
























3 readers' comments