Delve into the synthesis of Ambrox®, a substitute for ambergris in perfume, with this Chemistry Olympiad worked example question
In this question from the 2010 UK Chemistry Olympiad round one paper, students read about ambergris and its synthetic substitute, Ambrox®, before focusing on a proposed method of synthesising Ambrox® from a tree bark extract. They calculate the number of moles of Ambrox® produced each year, draw the structures of a range of compounds and calculate percentage yield. The accompanying video walkthrough is designed to help students if they get stuck or want to check their working.
The question is of moderate difficulty, and covers the following chemistry topics:
- Mole calculations
- Organic synthesis
- Yield calculations
What’s on this page?
- How to use this resource
- Question
- Answers
- Walkthrough (including video and transcript)
How to use this resource
Find out more about how to use Chemistry Olympiad worked answers.
Note
This question first appeared as question 1 in the 2010 UK Chemistry Olympiad round one paper. For marking, including notes on allowances, see question 1 in the 2010 examiners’ mark scheme.
Question
Ambergris, a metabolic product of the sperm whale, was for many years one of the most valuable ingredients in fine fragrances. Recently, it has been replaced with synthetic equivalents such as Ambrox® which possesses a powerful amber-type fragrance. Many different research groups have proposed methods for synthesising Ambrox® from natural products found in plants. A synthesis starting with (–)-drimenol extracted from the bark of the Chilean tree Drimys winteri is outlined below.
Part a
Given that ten tonnes of Ambrox® are produced every year, calculate the number of moles produced per year.
Part b
Draw the structures of compoundsA to D.
Part c
The yield of each step in the synthesis is shown beside the arrows in the scheme.
- What is the overall percentage yield of Ambrox® in this synthesis?
- What mass of (–)-drimenol would be needed each year if all of the commercially synthesised Ambrox® was made using this method?
- Given that Drimys winteri bark contains 0.5 % by mass of (–)-drimenol calculate the mass of bark that would be needed each year if all of the commercially synthesised Ambrox® was made using this method.
Answers
Part a
Ambrox® (C16 H28 O) has a molar mass of ((16 x 12.01) + (28 x 1.008) + (1 x 16)) = 236.384 g mol–1.
10000000 g produced every year, therefore (10000000/236.384) = 4.2 x 104 moles of Ambrox® are produced each year.
Part b
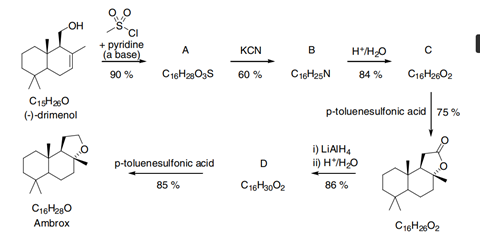
Compound A
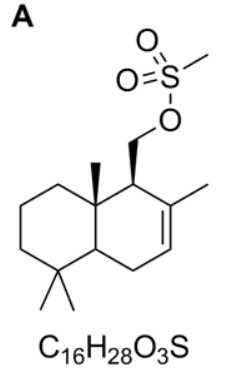
Compound B
As below or with the nitrile group shown as CN.
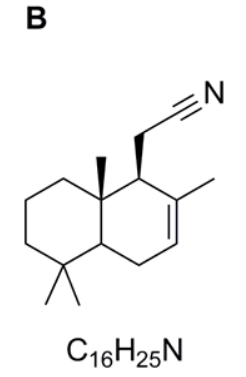
Compound C
As below or with the carboxyl group shown as COOH.
Compound D
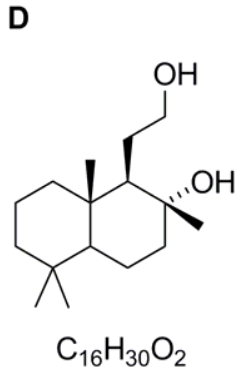
Part c
- The percentage yields for each step are combined to give an overall yield of 24.87%.
- 38 tonnes. This is calculated as follows:
- The number of moles of (–)-drimenol needed = (number of moles of Ambrox® produced in a year) / (overall yield) = (42304.5 / 0.2487) = 170102.5 moles of (–)-drimenol.
- (–)-drimenol has a molar mass of ((15 x 12.01) + (26 x 1.008) + (1 x 16)) = 222.358 g mol–1.
- The mass of (–)-drimenol needed is therefore (222.358 x 170102.5) = 38 tonnes.
- The mass of bark needed = (mass of (–)-drimenol) / (proportion of (–)-drimenol in bark) = 37.825 / 0.005 = 7.6 x 103 tonnes.
Walkthrough
Transcript
Download this
Introduction
This question is about a substitute for the perfume ingredient ambergris.
Ambergris is a metabolic product of the sperm whale and was for many years one of the most valuable ingredients in fine fragrances. Recently however, it has been replaced with synthetic equivalents such as Ambrox® which possesses a powerful amber-type fragrance. This question discusses one possible synthetic route to Ambrox® which starts from (–)-drimenol which can be extracted from the bark of a Chilean tree Drimys winteri.
Part a
Part (a) of the question, asks you to calculate the number of moles of Ambrox® produced per year given that 10 tonnes of Ambrox® are produced. This is a simple conversion of mass into moles which can be achieved using the equation moles = mass ÷ molar mass. However when using this equation, we need to take care with the units. Since the molar mass of a substance is the mass of one mole of that substance in grams, then we need to use the mass of the substance in grams. Since we are given the mass of Ambrox® in tonnes, we therefore need to convert the mass of Ambrox® in tonnes into a mass in grams. One tonne is equal to 1,000 kg which in turn is equal to 1,000,000 g. Therefore to convert tonnes into grams we need to multiply by a factor of 1,000,000.
To use our equation, we now need to know the molar mass of Ambrox®. This is the relative formula mass of Ambrox® in grams and can be calculated using the relative atomic masses for carbon, hydrogen and oxygen given in the periodic table at the start of the question. Completing the calculation, we calculate the molar mass of Ambrox® as 236.384 g mol–1. Placing our values now into the equation moles = mass ÷ molar mass, and remembering to convert the 10 tonnes of Ambrox® into grams, we calculate the number of moles of Ambrox® produced per year as 42,304. However, since the starting mass of Ambrox® is only given to 2 significant figures, 10 tonnes, then we can only give our final answer to the same degree of accuracy. Hence the number of moles of Ambrox® produced per year is 42,000 moles.
Part b
In part (b) of the question you are asked to look at the synthetic scheme for the conversion of (–)-drimenol into Ambrox® and give structures for compounds A–D. Much of the chemistry involved in synthetic schemes such as these may be new to you, but in many cases it is simply a matter of looking at the functional groups in the molecules and applying chemistry that you do know to slightly different situations.
If we do this for (–)-drimenol we can see that it contains a hydroxyl or alcohol group. Owing to the lone pairs of electrons on the oxygen atom, we know alcohols to be nucleophilic. Although you may not have seen the reagent, which is called methyl sulfonyl chloride before, you can see that it contains a chlorine atom which you will have seen is a good leaving group in nucleophilic substitution reactions. Hence you can envisage a similar reaction taking place in which the hydroxyl oxygen atom attacks the S of the methyl sulfonyl chloride and eliminates the chlorine atom as a chloride ion. This gives the structure of compound A as drawn.
In the next step, the reagent is potassium cyanide which you will have met as a source of the nucleophile, CN¯. When drawing a cyanide anion, note that it is nucleophilic on the carbon atom owing to the lone pair. The C–O bond has a dipole as a result of the electronegative oxygen atom and hence a nucleophilic substitution reaction occurs. The sulfonate anion is a good leaving group because it is very stable as a result of resonance of the negative charge with the S=O bonds. Therefore we can give the structure of compound B as the nitrile shown.
Compound B is then hydrolysed in acid. In this case you need to recognise that nitriles can be hydrolysed to carboxylic acids under acidic conditions and hence compound C is the carboxylic acid shown.
Compound C is then converted into the structure in the bottom right hand corner of the scheme under acidic conditions. Compound D is the product of the reaction of this cyclic ester with the reducing agent, lithium aluminium hydride, LiAlH4. Lithium aluminium hydride can be thought of as a source of hydride ions. Owing to the dipole in the carbonyl group, the carbonyl carbon atom of esters is susceptible to nucleophilic attack by the hydride ion to generate a tetrahedral intermediate. This tetrahedral intermediate is not stable and in molecules in which there is a good leaving group attached to the carbonyl carbon atom, can eliminates the leaving group (in this case the oxygen atom), reforming the strong carbonyl C=O in doing so. Therefore the first product from this reaction is the aldehyde shown.
However, the aldehyde also contains a carbonyl group which is highly susceptible to nucleophilic attack. Thus a second equivalent of hydride ion attacks the carbonyl group to generate the tetrahedral intermediate. However in this case, there is no good leaving group available and so the anion picks up a proton in the final work up stage to give the final structure of compound D as the alcohol drawn. In this question, you are not asked to give any mechanistic detail for the reactions involved – you are only required to draw the structures of the intermediates A–D. However, thinking through the mechanisms of the reactions involves helps to clarify the structures of each of the intermediates.
Part c
In part (c) of the question, you are asked to use the yield of the individual stages to calculate the quantity of tree bark needed for the annual synthesis of 10 tonnes of Ambrox®.
Part (1) asks you to calculate the overall percentage yield of Ambrox® in the synthesis given. If we look at the first step in which (–)-drimenol is converted into compound A, the yield of the reaction is 90%. When working with percentage yields note that it is always numbers of moles that is discussed and not masses. So, a yield of 90% means that one mole of (–)-drimenol reacts to produce 90% of 1 mole = 0.9 moles of Compound A. This 0.9 moles is then reacted with potassium cyanide to produce 60% of 0.9 moles = 0.6 × 0.9 moles = 0.54 moles of compound B. If we continue through the reaction sequence step by step in a similar vein, we can calculate the overall percentage yield of Ambrox® from (–)-drimenol in this synthesis as:
0.9 × 0.6 × 0.84 × 0.75 × 0.86 × 0.85 = 0.2486 or 24.9%
In part(2), you are asked to use this overall percentage yield to calculate the mass of (–)-drimenol which would be needed to the produce the 10 tonnes of Ambrox® produced per year. (–)-Drimenol reacts to produce Ambrox® in an overall yield of 24.9%. Remember that when discussing percentage yield we are discussing moles and not masses, we can therefore write that 24.87% = moles of Ambrox® / moles of (–)-drimenol × 100%. In part (a) of the question we calculated the number of moles in 10 tonnes of Ambrox as 42,304. Therefore, substituting this value into our equation we can determine the number of moles of (–)-drimenol needed for the annual production of Ambrox to be 170,109 moles.
The question however asks us for a mass of (–)-drimenol and so the final step of the calculation has to be to convert this number of moles of drimenol into a mass. Using the molecular formula of (–)-drimenol of C15H26O given in the question, we can calculate the molar mass of (–)-drimenol to be 222.358 g mol–1. Therefore using the equation, mass = moles × molar mass, we can calculate the mass of (–)-drimenol needed for the annual production of Ambrox® of 10 tonnes to be 37,825,097 g or 37.82 tonnes. Again we must give our final answer to the same degree of accuracy as the least accurate number in our calculation, and hence the mass of (–)-drimenol needed to produce 10 tonnes of Ambrox® is 38 tonnes. Notice that it is best to carry intermediate numbers through as much as possible on your calculator and then only give the final answer to the correct number of significant figures.
In the final part of the question, part (3) you are told that bark of the Drimys winteri tree contains 0.5% by mass of (–)-drimenol and asked to calculate the mass of bark that would be needed if all of the commercially synthesised Ambrox® was made using this method. In part (2), we calculated that the mass of (–)-drimenol needed was 38 tonnes. This 38 tonnes is therefore 0.5% of the mass of bark needed. Therefore the mass of tree bark needed can be calculated to be 7,565 tonnes or 7,600 tonnes to 2 significant figures.
Downloads
Organic synthesis and ambergris substitutes - video transcript
Editable handout | Word, Size 0.98 mbOrganic synthesis and ambergris substitutes - video transcript
Handout | PDF, Size 0.62 mb
Chemistry Olympiad worked answers
- 1
- 2
- 3
- 4
- 5
- 6
 Currently reading
Currently readingOrganic synthesis and ambergris substitutes
- 7
- 8
























No comments yet