Try this worked example of a Chemistry Olympiad question on the crystalline structure of gold and its unit cell
In this question from the 2010 UK Chemistry Olympiad round one paper, students encounter the cubic crystal structure of gold. They calculate the mass of one gold atom, before moving on to look in more detail at gold’s unit cell structure, its molar volume and atomic radius. They then extend these ideas to calculate the thickness and layers of gold covering the Dome of the Rock in Jerusalem.
The accompanying video walkthrough is designed to help students if they get stuck or want to check their working.
The question is of high difficulty, and covers the following chemistry topics:
- Mole calculations
- Unit cell calculations
What’s on this page?
- How to use this resource
- Question
- Answers
- Walkthrough (including video and transcript)
How to use this resource
Find out more about how to use Chemistry Olympiad worked answers.
Note
This question first appeared as question 6 in the 2010 UK Chemistry Olympiad round one paper. For marking, including notes on allowances, see question 6 in the 2010 examiners’ mark scheme.
Question
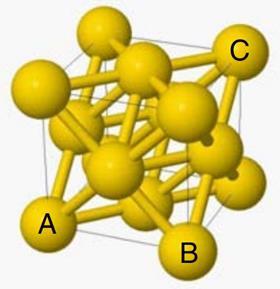
Gold atoms crystallise in the cubic arrangement shown in the figure on the right. The gold atoms, which are assumed to be spherical, are shown at half-radius size (rather than touching their neighbours) to illustrate the structure more clearly. The lattice structure can be built up from these cubic ‘building blocks’ – known as unit cells. Atoms are located at the corner positions and in the centre of the faces. The cube is shown as a thin outline; the thicker ‘bonds’ indicate which atoms are, in reality, in contact.
Avogadro’s constant is 6.02 × 1023 mol–1. Gold has only one isotope, which has a relative mass of 197. The density of gold is 19.3 g cm–3.
Part a
Calculate the mass (in g) of one gold atom.
Part b
The cube shown in wireframe in the figure has its corners at the centre of the atoms occupying those corner positions. The faces of the cube pass through the centre of the atoms found in the centre of the faces.
By considering the fraction of each atom actually inside the unit cell, calculate the number of atoms within the unit cell.
Part c
Bearing in mind that the atoms are in contact across the diagonal of a face of the cube, find expressions, in terms of the radius of the gold atom, r, for:
- The length of the edge of the unit cell, ie the distance between the centres of atoms A and B
- The volume of the unit cell
- The length of the unit cell body diagonal, ie the distance between the centres of the atoms A and C
Part d
Calculate the molar volume of gold in cm3 mol−1.
Part e
Given that the volume of a sphere is 4/3 πr3, calculate what fraction of the volume of the unit cell is occupied by gold atoms.
Part f
Bearing in mind your answer to part (e), calculate the radius of a gold atom.
Part g
A small mass of gold can be hammered out to cover an extremely large area with gold foil. The most efficient way of stacking layers of gold atoms has three layers in the length of the unit cell body diagonal, ie the thickness of one layer is one third of the distance A to C.
The great golden Dome of the Rock in Jerusalem is a hemisphere of diameter 21 m. The late King Hussein of Jordan donated 80 kg of gold to cover the outside of the dome.
- Given that the surface area of a sphere is 4πr2, calculate the average thickness in cm of the gold on the dome.
- Hence calculate the average number of layers of gold atoms covering the surface of the dome.
Answers
Part a
Mass of a gold atom = 197 g mol−1 / 6.02 ×1023 mol–1
= 3.27 × 10−22 g
Part b
Number of atoms in unit cell = (8 × 1/8) + (6 × 1/2) = 4
Part c
- If a is the length of the unit cell edge and r is the radius of an atom, a√2 = 4r. Length AB = 4r / √2 = 2√2 × r.
- Volume of unit cell = 32r3 / √2 = 16√2 × r3
- Length of body diagonal, a√3 = 2√6 × r
Part d
Molar volume of gold = 197 g mol−1 / 19.3 g cm−3
= 10.2 cm3 mol–1
Part e
Fraction = 4 × volume of gold atom / unit cell volume
= (4 × 4/3 πr3) / (16√2 × r3)
= π√2 / 6 = 0.74.
Part f
Radius of gold atom = [(volume of gold atom) / (4/3)π]1/3
= [(10.2 cm3 mol–1 / 6.02 × 1023 mol–1) × 0.74 / (4/3)π]1/3
= 1.44 × 10−8 cm
Part g
- Surface area of dome = ½ × 4π(21 m / 2)2 = 693 m2
Volume of gold = 80 000 g / 19.3 g cm−3 = 4 145 cm3 = 0.004 145 m3
Average thickness of gold = 0.004 145 m3 / 693 m2 = 6.0 × 10−6 m = 6.0 × 10−4 cm - Thickness of a layer of gold atoms = (2√6 × r) / 3 = 2.35 × 10−8 cm
Number of layers of gold atoms = 6.0 × 10−4 cm / 2.35 × 10−8 cm = 2.5 × 104
Walkthrough
Transcript
Download this
Introduction
This question is about gold leaf. The question begins by describing how gold atoms crystallise in a cubic arrangement which is shown. The gold atoms are assumed to be spherical and importantly, they are shown in the diagram at half-radius size, rather than touching their neighbours. The diagram shows a ‘unit cell’ which can be built up like ‘building blocks’ to form the lattice structure of gold.
Part a
In part (a) of the question, you are told that Avogrado’s constant is 6.02 × 1023 mol–1 and that gold has only one isotope, which has a relative mass of 197. You are then asked to use these facts to calculate the mass (in grams) of one gold atom. To answer this question you need to know two facts. The first is that one mole of any element contains Avogadro’s number of atoms. The second is that the mass of one mole of an element is equal to the relative atomic mass of that atom in grams. Therefore if the relative atomic mass of gold is given as 197, then we know that the mass of 6.02 × 1023 atoms of gold is equal to 197 g and hence the mass of one atom of gold is 197 g / 6.02 × 1023 atoms = 3.27 × 10–22 g per atom of gold.
Part b
In the next part of the question, you are told that the cube shown in the wire frame in the figure, which has now been highlighted in red, has its corners at the centre of the atoms occupying these corner positions. The faces of the cube pass through the centre of the atoms found in the centre of the faces.
In part (b), you are asked by considering the fraction of each atom actually inside the unit cell, to use this information to calculate the number of atoms within the unit cell. This question involves you looking at the diagram and trying to picture the unit cell in three dimensions. If we look then at the cube, if the faces of the cube pass through the centre of the atoms found in the centre of these faces, then the centre of each face each contains one half of an atom and so we can add ½ atoms to each of the six faces of the cube. Each corner of the unit cell contains one quarter of a half an atom which equals one eighth of an atom and so we can add a further one eighth of an atom to each of the corners of the unit cell. Therefore since each unit cell has 6 faces each containing one half of an atom and 8 corners each containing an eighth of an atom then we can calculate the total number of atoms within the unit cell to be 4.
Part c
Part (c) of the question now moves on to using trigonometry to calculate different dimensions of the unit cell, bearing in mind that the atoms are in contact across the diagonal of a face of a cube.
In part (1), you are asked to find an expression in terms of the radius of a gold atom, r, for the length of the unit cell which can be represented by the distance between the atoms A and B. If we look a single face of the unit cell we know that it has an atom at the centre of the face and atoms at each of the corners with the atoms touching across the diagonal. If the radius of a gold atom is given by r we can therefore see that the distance diagonally across the face of the unit cell is 4r.
To calculate the length of the edge of the unit cell, AB, we need to apply Pythagoras’ theorem. Pythagoras’ theorem states that in any right angled triangle, the square of the hypotenuse (the longest edge) is equal to the sum of the square of the two other sides. So in this case, as the unit cell is cubic and hence all sides are equal, we can say that (4r)2 is equal to 2 times AB2. Rearranging the equation and completing some simply algebra we can therefore give the length of the edge of the unit cell as 2√2r.
Part (2) now asks you to use this value to calculate the volume of the unit cell. Since the volume of a cube is equal to the length of one edge of the cube cubed, then the volume of the unit cell is simply (2√2r)3 which simplifies to 16√2r3.
Finally in part (3) of this part of the question, you are asked to give the length of the unit cell body diagonal, which is represented by the distance AC. In this case we need to look at what distances we already know and then use trigonometry to calculate the distance AC. If we look at the right angled triangle containing the diagonal AC, we know the length of one of the edges to be 2√2r. We don’t know the length of the other edge, represented in the diagram as AD but we can calculate it as it is the hypothenuse of a triangle with equal edges of length 2√2r. Therefore using Pythagoras, we can say the AD2 = 2 × (2√2r)2 which simplifies to AD = 4r. Knowing this distance, we can then apply Pythagoras a second time to the triangle ADC to determine the length of the unit cell body diagonal as 2√6r.
Part d
In part (d) of the question you are asked to calculate the molar volume of gold in cm3 mol–1. Initially you might be tempted to try a calculation using the volume of the unit cell calculated in part (c)(2). However, as we do not know r, the radius of a gold atom, it would not be possible to calculate a final answer. Instead, you need to look back at the start of the question where you were given a value for the density of gold of 19.3 g cm–3. The density of a substance is equal to the mass of that substance divided by its volume. So if we apply this equation to one mole of gold, we can state that 19.3 g cm–3 is equal to the mass of one mole of gold in grams divided by the volume of one mole of gold, or its molar volume in cm3. Since we know the mass of one mole of gold to be 197 g mol–1, we can rearrange the equation to give the volume of one mole of gold as the mass of one mole, 197 g mol–1 divided by the density of gold of 19.3 g cm–3, giving us a final answer for the molar volume of gold as 10.2 cm3 mol–1.
Part e
Part (e) of the question asks you to calculate what fraction of the volume of the unit cell is occupied by gold atoms. Since from part (b) we know that there are four atoms within the unit cell, and knowing that the volume of a sphere is given by 4/3πr3, then we can say that the volume of the unit cell occupied by atoms is 4 × 4/3πr3 = 16/3πr3. The total volume of the unit cell which contains these four atoms, we calculated in part (c)(2) as 16√2r3. Therefore we can give the fraction of the volume of the unit cell which is occupied by gold atoms as 16/3πr3 ÷ 16√2r3. Cancelling out the r3, the fraction of the volume of the unit cell which is occupied by gold atoms to be calculated to be 0.74.
Part f
Part (f) of the question then requires you to apply your answers to part (d) and part (e) to calculate the radius of a gold atom bearing. In part (d) you calculated the molar volume of gold to be 10.2 cm3 mol–1. In part (e) you calculated that 0.74 of this was occupied by gold atoms. Knowing this, we can therefore calculate the volume of one mole of gold atoms to be 0.74 × 10.2 cm3 = 7.55 cm3. Since one mole of gold contains Avogadro’s number of atoms, we can therefore calculate the volume of 1 atom as 7.55 cm3 ÷ 6.02 × 1023 = 1.25 × 10–23 cm3. Finally then, if the volume of a sphere is 4/3πr3 then 4/3πr3 = 1.25 × 10–23 cm3 and hence we can calculate r, the radius of a gold atom to be 1.44 × 10–8 cm which is approximately in the scale we would expect.
Part g
Part (g) of the question goes on to look at the application of gold to the Dome of the Rock in Jerusalem. In the introduction to part (g), you are told that the great golden Dome of the Rock in Jerusalem is a hemisphere with a diameter of 21 m and that the late King Hussein of Jordan donated 80 kg of gold to cover the outside of the dome.
In part (1) you are asked to calculate the average thickness in cm of gold on the dome. To calculate thickness, you need to divide the volume of gold used for the coverage by the surface area to be covered. Since we know the density of gold to be 19.3 g cm–3, we can calculate the volume of gold in 80 kg by dividing the mass of the gold in g, 80,000 g by its density 19.3 g cm–3. Hence the volume of 80 kg of gold is 4145 cm3. To calculate the area of the dome we need to use the equation for the surface area of a sphere given in the question of 4πr2. Since the diameter of the dome is 21 m or 2,100 cm, its radius is 1,050 cm. Therefore the surface area of the hemispherical dome is ½ of 4 × π × (1,050 cm)2 = 6,927,211 cm2. Therefore if 4145 cm3 of gold is used to cover an area of 6,927,211 cm2, then we can calculate that the thickness of the gold on the dome will be 4145 cm3 ÷ 6,927,211 cm2 = 5.98 × 10–4 cm. Since this calculation is based on the fact that the dome is covered by 80 kg of gold and that the diameter of the dome is 21 m, then we can only give our answer to 2 significant figures and so our final answer is that the thickness of gold on the dome will be 6.0 × 10–4 cm.
In part (2) of the question you are then asked to use this value to calculate the average number of layers of gold atoms covering the surface of the dome. At the start of part (g), you are told that the most efficient way of stacking the layers of gold atoms has three layers in the length of the unit cell diagonal, and therefore the thickness of one layer is one third of the distance from A to C. In part (c)(3) you calculated the length of the unit cell diagonal to be 2√6r. Substituting now the value for the radius of a gold atom, r, of 1.44 × 10–8 cm calculated in part (f) then the length of the unit cell diagonal in gold is 2√6 × 1.44 × 10–8 cm = 7.05 × 10–8 cm. Therefore the thickness of one layer of gold atoms is 1/3 × 7.05 × 10–8 cm = 2.35 × 10–8 cm. Finally then, if the average thickness of the gold on the dome is 5.98 × 10–4 cm and each layer of gold has a thickness of 2.35 × 10–8 cm, you can calculate the average number of layers of gold covering the surface of the dome as 5.98 × 10–4 cm ÷ 2.35 × 10–8 cm = 25,446 or 25,000 to 2 significant figures.
Downloads
The microscopic structure of gold leaf - video transcript
Editable handout | Word, Size 0.98 mbThe microscopic structure of gold leaf - video transcript
Handout | PDF, Size 0.65 mb
Chemistry Olympiad worked answers

Use these worked answers with video walkthroughs to challenge and support students learning to tackle Olympiad-style questions independently.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
 Currently
reading
Currently
reading
The microscopic structure of gold leaf
































1 Reader's comment